PEL SAC. GIOVANNI
BOSCO
Edizione Settima
TORINO, 1881
TIPOGRAFIA E
LIBRERIA SALESIANA
Sanpierdarena Nizza-Maritima-Buenos-Ayres-Montevideo
{1 [261]}
PROPRIETÀ
DELL’EDITORE {2 [262]}
INDEX
Al
benevolo lettore 3
I.
- Nozioni Preliminari e Numerazione. 3
II.
- Dell’Addizione. 5
III.
- Della Sottrazione 6
IV.
- Della Moltiplicazione. 8
V.
- Della Divisione. 11
VI
- Dei Numeri Decimali 13
VII
- Dell’Addizione Decimale. 14
VIII.
– Della Sottrazione Decimale 15
IX.-
Della Moltiplicazione dei Decimali 15
X.
- Della Divisione Decimale. 16
Del
sistema metrico decimale 18
XI.
- Nozione Generale di questo Sistema. 18
XII.
- Unità Fondamentali. 18
XIII.
- Multipli e Sottomultipli Decimali. 19
XIV.
- Lettura e Scrittura dei Numeri esprimenti misure Metrice Decimali. 20
XV.
- Delle Frazioni Ordinarie. 21
§.1.
Riduzione delle Frazioni a Minimi Termini. 23
§
2. Riduzione delle Frazioni allo stesso Denominatore. 24
§
3. Dell’Addizione delle Frazioni: 25
§.4
Della Sottrazione delle Frazioni. 25
§.5.
Della Moltiplicazione delle Frazioni. 26
§
6. Della Divisione delle Frazioni. 27
§.7.
Dei Numeri Complessi e Riduzione dei medesimi in Frazione Ordinaria e Decimale
e viceversa. 28
XVI.
- Della Regola del Tre. 29
XVII.
- Applicazioni della Regola del Tre nei Problemi d interesse e di Società
semplici 30
XVIII
- DEFIZIONE Delle Figure Geometriche Più Importanti 32
XIX.
- Geometria Solida 38
Appendice
I. Tavole dei Numeri Fissi e Maniera di usarle. 40
Tavola
1a - Piemonte-Torino 40
Tavola
2a - Lombardia-Milano. 41
Tavola
3a - Venezia. 42
Tavola
4a - Bologna 43
Tavola
5a - GENOVA. 43
Tavola
6a - Cagliari. 44
Tavola
7a - Parma. 44
Tavola
8a - Modena. 45
Tavola
9a - Firenze. 45
Tavola
10a - Roma. 46
Tavola
11a - Roma antica. 47
Tavola
12a - Napoli. 47
Tavola
13a - Palermo. 48
Appendice
II. Confronto fra le Monete di varii Stati d’Europa e delle Provincie d’Italia
colla Lira nuova o Franco. 50
Indice 52
Questo trattatello più volte stampato era assai diffuso; ma essendo esauste le varie edizioni non se ne curò più la ristampa. Oggi soltanto, ad invito di molti ed autorevoli personaggi, si riproduce a comodità delle scuole di campagna, degli artigiani e in generale per uso del corso elementare a norma dei programmi governativi per la pubblica istruzione.
Siccome non pochi fecero i loro studi prima che fosse in vigore il nuovo sistema, altri per motivo di commercio, o di pubblico impiego devono avere conoscenza dell’uno e dell’altro sistema; così per mezzo di tavole di confronto ognuno con un colpo d’occhio può conoscere le proporzioni di peso e misura antica colle nuove d’Italia. {3 [263]} Chi poi desiderasse di fare queste operazioni in modo ragionato, troverà pure i numeri fissi per la riduzione tanto dei pesi e delle misure, quanto dei rispettivi prezzi.
Mio scopo fu di essere breve, chiaro e di giovare ai figli del popolo. Se ci sono riuscito, se ne dia gloria al Datore di tutti i beni; se no, prego il lettore a voler gradire il mio buon volere e concedermi compatimento. Abbiate tutti vita felice. {4 [264]}
D. Che cosa è l’aritmetica?
R. L’aritmetica è la scienza dei numeri.
Siccome poi i numeri si uniscono e si dividono,
l’aritmetica si può definire la scienza del comporre e discomporre i numeri.
D. Che vuol dire numero?
R. Numero vuol dire unione di unità o di parti di unita.
D. Che cosa è quantità?
R. Dicesi quantità tutto ciò che si può considerare maggiore o minore.
La lunghezza di una strada, un’esercito, sono quantità perchè le possiamo considerare una lunghezza, un’essere più o meno grande.
D. Che vuol dire unità?
R. Unità vuol dire una cosa sola o considerata come sola, p. es: un libro, un calamaio, un anno, una tavola, un triangolo, un chilogramma, un popolo.
D. Come si formano i numeri?
R. I numeri si formano mettendo insieme più unità; o dividendo l’unità in parti.
Così aggiungendo una unità ad un’altra abbiamo il numero due; aggiungendone un’altra alle precedenti abbiamo il numero tre; dividendo l’unità in due, si avranno le metà; dividendola in tre, quattro ecc. si avranno i terzi, i quarti, ecc. Così si viene ad avere la serie illimitata dei numeri. {5 [265]}
D. Quante sorta di numeri vi sono?
R. Vi sono tre sorta di numeri: 1° numero intiero che contiene solo unità compiute, cosi: uno, quattro, dieci ecc. 2° il numero frazionario che contiene unità intiere e parte di unità p. es.: una mela e mezza. 3° la frazione che esprime soltanto parti di unità senza intieri p. es.: tre quarti d’ora, mezza libbra, ecc.
D. Come si possono ancora dividere i numeri?
R. I numeri si possono ancora dividere in astratti e concreti. Gli astr. sono quelli in cui non si indica il nome della specie a cui appartengono; p. es.: venti, quaranta, cento. - Conc, sono quelli in cui si indica il nome della specie, cui i numeri appartengono, come sarebbe venti anni, tre ore, cento scolari, ecc.
D. Come si potrà ritenere a memoria il nome di tutti i numeri interi?
R. Sarebbe molto difficile d’imparar l’aritmetica se tutti i numeri avessero un nome particolare. Per facilitare questa scienza si combinarono i numeri in modo che con pochi nomi si possano tutti nominare. Si divisero i numeri in unità, decine, centinaia in modo che dieci unità formano una decina, dieci decine un centinaio e dieci centinaia formano una unità di ordine superiore, che dicesi mille o migliaio. Dieci di queste unità di mila o migliaia formano una decina di mila, dieci decine di mila formano un centinaio di mila, dieci centinaia di mila formano una unità di ordine superiore ai mila, cioè un milione. E così si progredisce ai bilioni, trilioni ecc. Con questa divisione basta sapere solo i nomi delle unità semplici, delle decine e delle centinaia per poter pronunciare qualunque numero {6 [266]}
D. Quali sono i nomi delle unità, delle decine e delle centinaia?
R. Per le unità sono i seguenti: uno, due, tre, quattro, cinque, sei, sette, otto, nove. I nomi delle decine sono: dieci, venti, trenta, quaranta, cinquanta, sessanta, settanta, ottanta, novanta. I nomi delle centinaia sono: cento, duecento, trecento, quattrocento, cinquecento, seicento settecento, ottocento, novecento.
Oltre questi nomi hanno nomi proprii i numeri tra il dieci e venti e sono undici, dodici, tredici, quattordici, quindici, sedici, diciassette, diciotto, diciannove. Dal fin qui detto si vede che i numeri sono divisi in varii ordini; unità, mila, milioni, bilioni ecc. gli uni superiori agli altri, e che ogni ordine si suddivide in centinaia, decine ed unità.
D. Quale regola si ha da tenere per pronunciare i numeri?
R. Devesi sempre cominciare dall’ordine più grande e venir gradatamente ai più piccoli. In ciascun ordine poi si enuncieranno prima le centinaia, poi le decine, quindi le unità a cui si fa seguire il nome dell’ordine a cui appartengono, tacendo le unità, le decine e le centinaia che mancassero in qualsiasi ordine.
Così se un numero comprende quattro decine e tre centinaia di unità; ed inoltre sei decine e cinque unità di mila si pronuncierà nel modo seguente; sessantacinque mila, trecento quaranta {7 [267]}
D. Come si scrivono i numeri?
R. I numeri si scrivono con segni chiamati cifre.
D. Quante sono le cifre?
R. Le cifre che si adoperano ad esprimere i numeri sono nove:
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Uno
|
due
|
tre
|
quattro
|
cinque
|
sei
|
sette
|
otto
|
nove,
|
che chiamansi cifre
significative. A. queste si aggiunge lo O (zero), cifra per se stessa in
significativa, cioè che non esprime alcun numero, ma che serve a tenere il
posto delle cifre che mancano.
D. Come si scrivono i numeri che oltrepassano le nove unità?
R. Nello scrivere un numero qualunque si tiene la stessa regola che per pronunziarli; cioè, si cominciano a scrivere le centinaia, le decine, le unità dell’ordine maggiore; poi le centinaia, le decine, le unità dell’ordine immediatamente inferiore, finchè si arrivi alle unità semplici; coll’avvertenza però di scrivere dei zeri al posto delle centinaia, decine od unità mancanti in qualsiasi ordine. Sia da scriversi in cifre il numero trentacinque mila duecento sei. Si comincierà a scrivere l’ordine maggiore, che qui è quello dei mila. Non essendovi centinaia di mila, si scriveranno le tre decine e le cinque unità di mila; poscia si scriverà l’ordine delle unità cominciando a notare le due centinaia, uno zero per le decine che nel numero proposto non vi sono, quindi le sei unità semplici; così si avrà 35, 206.
D. Qual regola tenere nel leggere i numeri?
R. Si separano le cifre che li compongono di tre in {8 [268]} tre andando da destra verso sinistra. La prima casella conterrà le unità, la seconda i mila, la terza i milioni ecc. L’ultima casella potrà avere meno di tre cifre. Quindi si comincierà da sinistra a leggere il numero contenuto in ciascuna casella come se fosse solo, aggiungendo in fine di ciascuna casella il nome dell’ordine che rappresenta.
Sia da leggere il numero 31405078. Dividendo il numero da destra a sinistra di tre in tre cifre si avrà:
|
milioni
|
mila
|
unità
|
|
31
|
405
|
078
|
La prima casella a destra esprime le unità, la seconda i mila, la terza i milioni. Cominciando pertanto a sinistra a leggere il numero di ciascuna casella come se fosse solo, si dirà: trentun milioni quattrocento cinque mila e settantotto.
D. Quanti valori può avere una cifra?
R. Due: l’assoluto e il relativo. L’assoluto è quel valore che ha la cifra per se stessa indipendentemente dal posto che occupa. Il valore relativo è quello, che la cifra acquista secondo il posto che occupa nella scrittura di un numero. Così per es.: nel numero 68 il valore assoluto della prima cifra a sinistra è sei, il valore relativo è sei decine ossia sessanta.
D. Come si chiama la parte di aritmetica che insegna a formare, leggere e scrivere i numeri?
R. Si chiama numerazione.
D. Che cosa è adunque la numerazione e come si divide? {8 [269]}
D. Che cosa è la numerazione parlata?
R. Dicesi numerazione parlata la maniera di formare i numeri e di esprimerli con parole.
D. Che cosa è la numerazione scritta?
R. Dicesi numerazione scritta la maniera di rappresentare i numeri con pochi segni detti cifre.
D. Quali sono le operazioni fondamentali dell’aritmetica?
R. Le operazioni fondamentali che formano la base di tutta l’aritmetica sono: l’addizione, la sottrazione, la moltiplicazione e la divisione.
ESERCIZI
SULLA NUMERAZIONE.
Si scrivano in cifre diciassette franchi. Cento venticinque giovani virtuosi. Mille dugento tegole.
La città di Torino conta circa duecento ventimila abitanti.
Mille e cinquecentosei miria di legna; ottanta mila
militari valorosi.
Si leggano i numeri seguenti: 800 miriagrammi di uva. Nella
battaglia di Lepanto fu disfatta dai cristiani un’armata di oltre 50000 mila
Turchi. Nelle persecuzioni oltre a 18000000 di cristiani diedero la vita per la
fede.
D. Che cosa è l’addizione?
R. L’addizione è un operazione con cui si uniscono due o più numeri della medesima specie per vedere quanto formino presi insieme.
I numeri che si devono unire si dicono poste.
Il numero che risulta dall’unione delle poste si chiama somma o totale.
D. Non si possono unire insieme i numeri di specie diversa?
R. I numeri di specie diversa non si possono unire insieme. {10 [270]} Così p. es. se dico: 25 franchi e 60 chilogrammi, bisogna considerare le somme separatamente. Se poi dico: 25 franchi e 50 franchi, si possono unire insieme appunto perchè sono della medesima specie.
D. Che cosa bisogna osservare intorno all’addizione?
R. Per fare l’addizione bisogna osservare attentamente che le cifre delle varie poste vengano scritte in maniera, che le unità siano scritte sotto alle unità, le decine sotto alle decine, le centinaia sotto alle centinaia, ecc.
ESEMPIO: - Dovendo scrivere 513 e 85 si disporranno i numeri così:
|
Prima
posta
|
513
|
|
Seconda
posta
|
85
|
Nel che dobbiamo badare che il
numero 5 venga scritto sotto al 3 e l’8 sotto all’1.
Disposti così i numeri e tirata una linea orizzontale, si farà l’operazione nel modo seguente:
|
Prima posta
|
513
|
Si comincierà
dalla destra,
|
|
Seconda posta
|
85
|
cioè dalla
colonna delle unità
|
|
Linea orizzont
|
-------
|
semplici
dicendo: 5 più 3 danno
|
|
Totale
|
598
|
otto, e
scriveremo 8. Poi si passa alla colonna delle decine dicendo: 8 e i fanno 9 e
scritto 9, si dirà 5 resta 5. Il totale sarà 598.
|
Osservazione. - Se i numeri della stessa colonna presi insieme fanno 10 si scriverà
0 nella colonna delle unità e si porterà uno nella colonna delle decine.
In generale nel sommare, quando i numeri presi insieme formano una o più decine, si scriverà soltanto l’ultima cifra cioè quella delle unità, e le decine considerate come unità verranno trasportate nella colonna che segue.
ESEMPIO:
|
Prima posta
|
389
|
|
Seconda posta
|
154
|
|
Terza posta
|
392
|
|
|
----------------
|
|
Totale
|
935
{11 [271]}
|
Cominciando dalla
posta inferiore si dirà: 2 più 4 fanno 6, più 9 danno 15. Si scriverà 5 sotto
le unità, e si trasporterà uno nella colonna delle decine dicendo: 1 più 9
fanno 10, più 5 danno 15, più otto eguagliano 23. Si scrive 3 sotto alla
colonna delle decine e si porterà 2 nella colonna delle centinaia (questi due
eguagliano 20 decine ovvero dugento unità}: indi si continuerà: 2 più 3 fanno
5, più 1 fa 6, più 3 fanno 9. Il totale sarà 935.
D. Con qual segno viene indicato che due numeri sono da addizionarsi?
R. Ciò viene indicato con una piccola croce + che dicesi più e si mette fra i numeri che si devono unire.
Così 3+4 ci indicherà che il 3 si deve addizionare col 4 e si dirà 3 più 4 uguale a 7, la quale parola uguale a si esprimerà con due tratti di linea orizzontale in questo modo 3+4 = 7.
D. Come si fa la prova dell’addizione?
R. Per fare la prova dell’addizione si sommano nuovamente le poste, ma in modo inverso, cioè cominciando dal basso se prima si era cominciato dall’alto, oppure dall’alto, se si era cominciato dal basso. Se il secondo totale è uguale al primo, l’operazione si può credere esatta.
ESERCIZI
SULL’ADDIZIONE.
1° Un padrone pagò fr. 750 per fitto di bottega. Più 560 come stipendio annuo a due operai. Più 130 ad un apprendizzo che aveva mostrato speciale diligenza nel servirlo. Quanto ha speso in tutto?
2° Un falegname ha speso in assi fr. 1526; in travi 2847; in comperar utensili 235. Quanto ha speso in tutto?
3° Un contadino ha speso per la propria famiglia in abiti fr. 300; in frumento 150; in meliga 367. Quanto ha speso in tutto?
4° Un padre per mantener suo figlio in collegio spende fr. 450 di pensione, fr. 215 in abiti, calzamenta e riparazioni, fr. 97 in libri e carta. Quanto spende in tutto? {12 [272]}
D. Che cosa è la sottrazione?
R. La sottrazione è un’operazione per cui si leva un numero da un altro per conoscere quanto resti.
D. Quali nomi soglionsi dare ai numeri nella sottrazione?
R. Il numero che si vuol diminuire, appellasi minuendo; quello che si vuol levare dal prima dicesi sottraendo, il numero che resta si nomina residuo o differenza.
D. Si può far la sottrazione quando il minuendo è di specie diversa dal sottraendo?
R. In quel modo che non si possono sommare numeri di specie diversa, cosi non si possono sottrarre.
D. Come si fa la sottrazione?
R. Per fare la sottrazione si scrivono le cifre del sottraendo sotto a quelle del minuendo in modo, che le unità siano scritte sotto alle unità e le decine sotto alle decine ecc.: tirata poi una linea, si comincia dalla destra a sottrarre le unità dalle unità e le decine dalle decine, scrivendo il residuo al di sotto della linea: lo stesso si farà colle altre cifre andando verso sinistra, finchè sia finita l’operazione.
ESEMPIO:
Un padre paga 525 franchi per pigione annua di casa, ne ha già pagato 313; quanto deve ancora pagare?
|
Minuendo L.
|
525
|
Per fare questa
operazione si levano 3 da 5;
|
|
Sottraendo L.
|
313
|
e si dirà: chi
di 5 paga 3 restano 2, i quali
|
|
Linea orizzon.
|
-
|
scriviamo sotto
alla linea. Chi di 2 paga 1
|
|
Residuo L.
|
212
|
resta 1, che
scriviamo pure sotto la linea. Chi di 5 paga 3; restano 2. Il residuo saranno
fr. 212.
|
D. Che cosa bisogna osservare nella sottrazione?
R. Per capire i varii casi della sottrazione bisogna osservare: 1. Che quando la cifra del sottraendo è uguale {13 [273]} alla cifra corrispondente del minuendo, scriveremo 0 sotto la linea: 2. Quando la cifra del sottraendo è maggiore della cifra corrispondente del minuendo, allora si prenderà una unità dalla prossima cifra del minuendo a sinistra, la quale unità essendo una decina rispetto al posto ore si porta, avrà il valore di dieci.
ESEMPIO:
Un signore comperò un podere che costò L. 3405, ne ha già pagato 1605. Quanto deve ancora pagare?
|
Min.
|
3405
|
L’operazione si
farà così: 5 meno 5 resta nulla, si scrive 0
|
|
Sottr.
|
1605
|
nel residuo; 0
meno 0 resta 0: si scrive 0 nel residuo; 4
|
|
Linea
|
|
meno 6 oppure
chi da 4 leva 6, leva troppo, perciò
|
|
Residuo
|
1800
|
si prende una
unità dal 3, che rispetto al 4, essendo decina, varrà 10 unità, e addizionata
insieme risulterà 14; 14 meno 6 resta 8; scriviamo 8 nel residuo. Ora dal 3
avendone preso 1, resta 2, e si dirà 2 meno 1 resta 1. Il residuo sarà 1800.
|
D. Come si fa la sottrazione quando s’incontrano uno o più 0 nel minuendo?
R. Quando nel sottraendo c’è una cifra significativa e nel minuendo s’incontra uno 0, allora lo 0 si conta come 10, e la prima cifra che s’incontra a sinistra diminuisce di uno. Se poi occorrono più 0 uno dopo l’altro si terrà questa regola. Il primo 0 si conta per 10, gli altri si contano solamente per nove; ma la prima cifra significativa che s’incontrerà a sinistra si diminuirà di uno.
ESEMPIO:
Un panattiere aveva un capitale di franchi 3500; ha già speso in frumento fr. 1327. Quanto gli rimane ancora?
|
|
Min. 3500
|
|
|
Sottr.1327
|
|
|
Residuo 2173 {14
[274]}
|
D. Come si indica che un numero si deve sottrarre da un altro?
R. S’indica con una lineetta orizzontale - (che si esprime colla parola meno), posta fra il numerò minuendo ed il sottraendo.
Così dovendosi sottrarre 5 dal 7, si fa la sottrazione scrivendo 7-5=2, e si dirà sette meno cinque uguale a due.
D. Come si fa la prova della sottrazione?
R. Per fare la prova della sottrazione, si somma il residuo col sottraendo. Se la somma totale risulta uguale al minuendo l’operazione è esatta.
ESEMPIO:
Un impresario deve provvedere 20550 mattoni; ne ha già provveduto 12500. Quanti ne deve ancora provvedere?
|
Min. 20550
|
|
Sottr. 12500
|
|
Residuo 8050
|
|
Prova 20550
|
ESERCIZI
SOPRA LA SOTTRAZIONE.
1° Un contadino ha il reddito annuo di lire 2650; ne paga 725 per un suo figlio studente all’università; quanto gli resta ancora per la famiglia?
2° La città di Roma sul principio dell’anno contava di popolazione circa 290 000, sul finire si trovano registrati nel libro dei morti 8187; quanti rimangono ancora?
3° Un uomo che dovesse vivere sino a 86 anni e 11 mesi, 18 ore quanto gli rimarrebbe da vivere quando si trova all’età di anni 77 e mesi 8, ore 16? {15 [275]}
D. In che consiste la moltiplicazione?
R. La moltiplicazione consiste nel ripetere tante volte un numero detto moltiplicando quante sono le unità di un altro numero detto moltiplicatore.
Il moltiplicando ed il moltiplicatore soglionsi appellare col nome di fattori. Il fattore maggiore si suole scrivere il primo.
Ciò che risulta dall’operazione dicesi prodotto.
Per imparar la moltiplicazione bisogna esercitarsi alla lettura della tavola seguente:
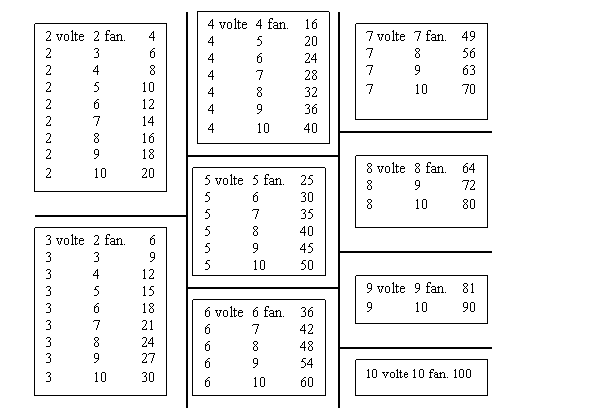
{16 [276]}
Si può anche imparar bene la moltiplicazione studiando quest’altra tavola detta Pitagorica dal nome del suo inventore che si chiama Pitagora.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
20
|
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
30
|
|
4
|
8
|
12
|
16
|
20
|
24
|
28
|
32
|
36
|
40
|
|
5
|
10
|
15
|
20
|
25
|
30
|
35
|
40
|
45
|
50
|
|
6
|
12
|
18
|
24
|
30
|
36
|
42
|
48
|
54
|
60
|
|
7
|
14
|
21
|
28
|
35
|
42
|
49
|
56
|
63
|
70
|
|
8
|
16
|
24
|
32
|
40
|
48
|
56
|
64
|
72
|
80
|
|
9
|
18
|
27
|
36
|
45
|
54
|
63
|
72
|
81
|
90
|
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
Essa contiene tutti i prodotti in cui i fattori sono di una sola cifra. Per trovare questi prodotti si deve tenere la seguente regola: Si cerca uno dei fattori nella prima linea superiore, e l’altro nella 1a colonna a sinistra, il prodotto si troverà nella casella d’incontro della colonna che passa pel 1° fattore e della linea che passa pel 2°. Cosi per es. voglio il prodotto di 5 moltiplicato 8: Cerco 5 nella linea superiore e vedo che è nella 5a colonna, e poi cerco 8 nella prima colonna e vedo che si trova nella prima casella della ottava linea. Ora osservo dove s’incontra là 5a colonna coll’ottava linea e vedo che s’incontra nella casella del 40: allora si dirà 5 moltiplicato per 8=40 {17 [277]}
D. Come si fa la moltiplicazione?
R. Scritto il moltiplicatore sotto al moltiplicando, si tira una linea, indi si prende ciascuna cifra del moltiplicando tante Tolte, quante sono le unità del moltiplicatore, e quando il prodotto oltrepassa il dieci, si scrivono soltanto le unità, e le decine si uniscono al prodotto della cifra seguente.
ESEMPIO: - Quale prodotto dà 453 moltiplicato per 3?
|
Moltiplicando
|
453
|
Cominciando
dalla destra si andrà a sinistra
|
|
Moltiplicatore
|
3
|
dicendo:3 volte
3 danno9, scriveremo9 nel
|
|
Prodotto
|
1359
|
prodotto: 3
volte5 danno 15, porremo5 e porteremo una decina nel prodotto seguente; 3
volte 4 danno 12, più 1 che abbiamo portato, dà 13 che si scrive per intero
non essendovi più nulla da moltiplicare. Avremo per prodotto 1359.
|
D. Come si fa la moltiplicazione quando nel moltiplicatore ci sono più cifre oppure occorrono zeri?
R. Quando nel moltiplicatore ci sono due o più cifre, allora si moltiplica ciascuna di esse cifre per tutto il moltiplicando, e còsi si avranno tanti prodotti quante sono le cifre nel moltiplicatore. Tali prodotti si dicono parziali; ma avverti di scriverli in modo, che ciascun prodotto parziale abbia la sua prima cifra sotto alla cifra corrispondente del moltiplicatore. Poscia si sommano insieme tutti i prodotti parziali. Qualora poi occorrano zeri nel moltiplicatore, non si fa altro che scrivere sotto ai medesimi un altro zero nel prodotto e si passa subito alla cifra susseguente.
ESEMPIO:
Un agente di campagna spende ogni giorno in operai franchi 280: Quanto spenderà in un anno, ovvero in giorni 365?
|
Moltiplicando
|
365
|
|
Moltiplicatore
|
280
|
|
Primo prod.
|
29200
|
|
Secon. prod.
|
730
|
|
Prodotto tot.
|
102200
|
Si dirà 0 moltiplicato per 5 dà 0; si scrive 0 nel prodotto sotto allo 0; 8 moltiplicato per 5 dà 40, scriviamo 0 sotto allo {18 [278]} stesso 8, e porteremo 4 decine dicendo: 8 moltiplicato per 6dà 48, più 4 che portavamo, danno 52; si scrive 2 e si portano 5 decine dicendo: 8 moltiplicato per 3 dà 24 più 5, che portavamo, diano 29, si depone tutto il 29. Il primo prodotto sarà 29200. Si passa alla terza cifra del moltiplicando dicendo: 2 moltiplicato per 5 dà 10, si depone 0 nel secondo prodotto, ma sotto al 2, si porterà una decina dicendo: 2 moltiplicato per 6 dà 12 più uno, che portavamo, fanno 13; si scrive 3 e si porta una decina dicendo: 2 moliiplicato per 3, dà.6, più uno che portavamo avremo 7. Il secondo prodotto sarà 730. Sommando questi due prodotti insieme si avrà il prodotto totale 102200.
D. Come si fa la moltiplicazione di un numero intero per 10, per 100, per 1000 ecc.?
R. Basta aggiungere uno 0 a qualunque numero e sarà moltiplicato per dieci, per cento se ne aggiungo due, per mille se si aggiungeranno tre 0 e così via.
Così 3 moltiplicato 10 darà 30; 3 moltiplicato 100 darà 300. Questo avviene pel principio che un numero acquista un valore di 10 in 10 volte più grande, per ogni cifra che si avanza da destra verso a sinistra.
D. Quando si ha da far uso della moltiplicazione?
R. Quando conoscendo quanto vale un’unità; si cerca il valore di più unità.
Così per es.: sappiamo che un metro di panno costa 8 lire, e cerchiamo quanto costano 15 metri. Come pure: sappiamo che un giorno equivale a 24 ore e vogliamo sapere a quante ore equivalgono 6 giorni, ossia quante ore vi siano in 6 giorni.
D. Come si indica che due numeri si devono moltiplicare tra di loro?
R. Mettendo fra di essi il seguente segno x formato con due lineette trasversali, che dicesi moltiplicato. Così avendo da moltiplicare il 3 per 4 si scriverà 3x4 = 12, e si dirà: tre moltiplicato quattro uguale a dodici.
D. Come si fa la prova della moltiplicazione?
R. La maniera più semplice e facile per fare la prova della moltiplicazione è di mettere il moltiplicando al posto del moltiplicatore e ripetere la moltiplicazione. {19 [279]} Se i due prodotti saranno uguali, si può credere che la moltiplicazione sia esatta.
Cosi per esempio: 12x20 = 240; cambiando l’ordine dei fattori avremo 20x12 = 240: Que to secondo prodotto eguale al primo ci indica che l’operazione è ben fatta.
ESERCIZI
SULLA MOLTIPLICAZIONE.
1° Un figlio consuma per settimana in fumare tabacco 2 fr., nel bigliardo fr. 5, quando avrebbe in fine dell’anno astenendosi da tali vizi?
2° Una madre comperò 219 metri di panno a fr. 8 il metro: quanto deve pagare?
3° Ogni giorno è di 24 ore, ogni ora è di 60 minuti, quante ore e quanti minuti ci sono in un giorno, in una settimana, in un mese, in un anno ossia in giorni 365?
4° Quanto si deve pagare per 85 ettolitri di vino a franchi 23 all’ettolitro?
D. Che cosa s’intende per divisione?
R. Per divisione s’intende un’operazione colla quale si cerca quante volte un numero chiamato divisore sia contenuto in un altro chiamato dividendo. Il numero che risulta chiamasi quoziente. Il dividendo ed il divisore chiamansi anche termini della divisione,
D. Come si fa la divisione?

 R. Si scrive il dividendo, che vie/i separato dal divisore
per mezzo di una linea orizzontale e di un’altra verticale come nella figura
seguente quindi si prendono a sinistra del dividendo tante cifre, quante
sono nel divisore e si osserva quante volte questo sta nelle cifre prese nel
dividendo. La parte che risulta scrivesi sotto al divisore e dicesi quoziente.
{20 [280]} Questo si moltiplica pel divisore e il prodotto scrivesi sotto alle
cifre prese nel dividendo da cui si fa la sottrazione. Il resto bisogna sempre
che sia minore del divisore, altrimenti la cifra trovata del quoziente sarebbe
troppo piccola.
R. Si scrive il dividendo, che vie/i separato dal divisore
per mezzo di una linea orizzontale e di un’altra verticale come nella figura
seguente quindi si prendono a sinistra del dividendo tante cifre, quante
sono nel divisore e si osserva quante volte questo sta nelle cifre prese nel
dividendo. La parte che risulta scrivesi sotto al divisore e dicesi quoziente.
{20 [280]} Questo si moltiplica pel divisore e il prodotto scrivesi sotto alle
cifre prese nel dividendo da cui si fa la sottrazione. Il resto bisogna sempre
che sia minore del divisore, altrimenti la cifra trovata del quoziente sarebbe
troppo piccola.
I seguenti esempi insegneranno il modo di fare la divisiono:
Un padrone vuole regalare fr. 92 a 4 suoi garzoni pel buon capo d’anno; quanto avrà ciascuno.
|
Dividendo
92
|
4 divisore
|
|
|
8
|
23 quozient
|
|
|
12
|
|
|
|
12
|
|
|
|
00
|
|
Scritto il divisore a destra del dividendo come sopra, si osserverà quante volte il divisore stia nella prima cifra del dividendo, e diremo: il 4 nel 9 sta due volte e si scrive 2 nel quoziente sotto il divisore; per non confondere l’operazione bisogna subito separare il 9 con una virgola in alto per significare, che si è già preso. Lo stesso si osserverà per tutte le altre cifre. Quindi si moltiplichi il quoziente 2 pel divisore 4, e avremo 8. Questo 8 si scrive sotto al 9 del dividendo e si farà la sottrazione dicendo 9 meno 8 resta 1. Si proseguirà: accanto a questo uno si abbassa l’altra cifra del dividendo, che è 2, e si porrà a destra dell’1 che essendo una decina farà 12. Ora si dirà: il 4 nel 12 sta 3 volte; si metterà 3 nel quoziente a destra del 2 e moltiplicando 3 pel divisore 4 si avranno 12, che scriveremo sotto al 12 del dividendo: e, fatta la sottrazione, si avrà 0. Il quoziente ovvero la parte che toccherà a ciascuno è 23 franchi.
Osservazione. - Quest’operazione serve di norma quando il divisore è contenuto nella prima cifra del dividendo.
D. Come si fa la divisione quando il divisore non può essere contenuto nella prima cifra del dividendo?
R. Quando il divisore non può essere contenuto nella prima cifra del dividendo, allora si prenderanno due cifre. {21 [281]}
ESEMPIO:
|
Dividendo
130
|
5 divisore
|
|
|
10
|
26 quoziente
|
|
|
30
|
|
|
|
30
|
|
|
|
00
|
|
Si dirà: il divisore 5 non istà nella prima cifra del dividendo 1, perciò si prenderà anche la cifra seguente che fa 13. Ora il 5 nel 13 entra 2 volte; si scriva 2 nel quoziente; 2 moltiplicato per 5 dà 10, si scriverà 10 sotto al 13, e si farà la sottrazione; nel resto si opererà come sopra.
D. Come si fa la divisione quando nel divisore ci sono più cifre?
R. Quando nel divisore vi sono più cifre, si prendono tante cifre del dividendo, quante sono nel divisore, e quando il valore delle cifre del divisore supera quello delle cifre del dividendo in numero eguale, si prenderà una cifra di più nel dividendo.
ESEMPIO:
|
Dividendo
450
|
25 divisore
|
|
|
25
|
18 quozient
|
|
|
200
|
|
|
|
200
|
|
|
|
000
|
|
Il due che è la prima cifra del divisore sta due volte nella prima cifra del dividendo; ma il 5 che è la seconda cifra del divisore non istà più due volte nel 5 del dividendo; perciò si dirà: il 2 nel 4 sta una volta col residuo di 2 che uniti al 5 fanno 25. Il 5 del divisore sta anche abbondantemente una volta nel 25: onde si scriverà uno nel quoziente. Indi si moltiplica il quoziente 1 pel divisore 25 e si avrà per prodotto 25, che si scrive sotto al 45. Fatta la sottrazione si avrà.20 ed accanto di esso si abbasserà l’ultimo 0 del dividendo per cui risulterà 200.
Qui il 25 non potendo essere contenuto in un numero uguale di cifre, bisognerà prenderne una di più; vale a dire invece di 20 si prenderà 200; dicendo: il due sta nel 2 del diridendo, ma il 5 non istà più nelle cifre seguenti, perciò si dirà: il 2 nel 20 {22 [282]} sta 8 volte; avverti però che il 2 nel 20 starebbe 10 volte, ma non deve mai oltrepassare le nove volte, perchè si tratta di cercare per quoziente una sola cifra alla volta e non due, e nemmeno il 2 nel 20 può stare 9 volte, perchè non dà un residuo sufficiente, il quale unito allo zero possa contenere il 5 anche nove volte. Perciò diremo il due nel 20 sta 8 volte col residuo di 4, che unito allo 0 fa 40. Ora il 5 nel 40 sta anche 8 volte e si scriverà otto nel quoziente, il quale 8 moltiplicato per 25 darà 200. Fatta poi la sottrazione, si avrà 000 di resto. Nel quoziente avremo 18.
Osservazione. - Se nel decorso dell’operazione, dopo aver abbassata una cifra del dividendo, non basta per contenere il divisore, si scriverà zero nel quoziente e si abbasserà un’altra cifra dello stesso dividendo.
D. Come si fa per dividere per 10, 100, 1000 ecc. un numero terminato per zeri?
R. Se si vuol dividere per 10 si toglie uno zero ed il numero che vi resta sarà il quoziente. Se si vuol dividere per 100 si tolgono due zeri, per 1000 se ne tolgono tre.
Così il numero 20000 diviso per 10 darà per quoziente 2000; diviso per 100 darà 200, diviso per 1000 darà 20. Ciò avviene pel principio che una cifra prende un valore di 10 in 10 volte più piccolo a misura che si avanza da sinistra verso destra.
D. Quando si deve usare la divisione?
R. Si usa la divisione:
1° Quando dato il valore di più unità ed il numero di queste unità, si cerca quanto vale una sola.
Così per es. 25 metri di panno costarono lire 300, si cerca quanto costò un metro.
2° Quando dato il valore di più unità ed il valore di una sola si cerca quante sono queste unità.
Per es. si hanno 450 lire per comprare stoffa che costa lire 9 al metro; si desidera sapere quanti metri se ne possono comprare. {23 [283]}
D. Come si indica che un numero è divìso per un altro?
R. Si indica col segno di due punti (diviso per) posto fra il dividendo e il divisore.
Così per indicare che si vuole dividere il 9 per 3 si scriverà 9:3=3 e si dirà nove diviso per tre è uguale a tre.
D. Come si fa la prova della divisione?
R. La prova della divisione si fa moltiplicando il quoziente pel divisore, e aggiungendo il residuo se vi è. Se la somma eguaglierà il dividendo, l’operazione sarà ben fatta.
ESEMPIO:
|
Dividendo
441
|
7 divisore
|
|
|
42
|
63 quozient
|
|
|
21
|
7
|
|
|
|
21
|
441
|
|
|
|
00
|
|
Per fare la prova nel proposto esempio si moltiplica il quoziente 63, pel divisore 7 e dando 411, che è somma uguale al dividendo, l’operazione è esatta.
Se la divisione terminasse con un resto, bisognerà aggiungerlo al prodotto perchè questo diventi eguale al dividendo.
ESERCIZI
SULLA DIVISIONE.
1° Un siguore mosso da vero spirito di carità assegna fr. 216 da distribuirsi a 9 povere famiglie. Quanti fr. toccheranno a ciascuna?
2° Un ragazzo generoso vuole regalare 500 noci a 20 suoi compagni; quante ne avrà ciascuno?
3° Un padre di famiglia ha 2190 fr. di reddito annuo: quanto può spendere al giorno onde averne per tutto l’anno ovvero per giorni 365? {24 [284]}
D. Quali sono i Numeri Decimali?
R. Sono quei numeri che esprimono intieri e parti, di unità successivamente di 10 in 10 volte più piccole.
D. Come si chiamano quei numeri che indicano solo parti di 10 in 10 volte più piccole dell’unità?
R. Si chiamano frazioni decimali.
D. Che cosa devesi specialmente osservare nella numerazione decimale?
R. Nella numerazione decimale bisogna separare le frazioni dalle unità intere per mezzo di una virgola.
Per esempio se voglio scrivere 25 franchi, più 50 centesimi scriverò 25, 50.
D. Le cifre poste dopo la virgola, qual parte dell’unità esprimono?
R. La prima cifra dopo la virgola esprime i decimi dell’unità che precede, la seconda i centesimi, la terza i millesimi, la quarta i diecimillesimi, la quinta i centomillesimi, la sesta i millionesimi e così di seguito.
Siano metri 42,356. Il numero 42 esprime le unità; il 3 perchè è la prima dopo la virgola, esprime i decimi del metro; il 5 i centesimi, il 6 i millesimi. Perciò per esprimere i decimi basterà una sola cifra dopo la virgola, per esprimere i centesimi ce ne vogliono due, pei millesimi tre, pei diecimillesimi quattro e cosi di seguito. {25 [285]}
D. Come si scrivono i numeri decimali?
R. Si comincia a scrivere il numero intero, se vi è, e se non vi è si mette uno 0, per indicare che non vi sono unità; dopo si pone la virgola; poscia si osserva quante cifre ci vogliono per esprimere quella sorta di frazione decimale che è contenuta nel numero proposto. Se la frazione decimale considerata come numero intero non arriva allo stesso numero di cifre, si supplisce con zeri subito dopo la virgola.
Sia da scrivere zero interi e venticinque millesimi. Per esprimere i millesimi ci vogliono tre cifre, e per scrivere venticinque ce ne vogliono solo due; perciò si metterà subito dopo la virgola uno zero in questo modo 0, 025.
D. Come si leggono i numeri decimali?
R. Si cominciano a leggere i numeri interi, poi si legge la frazione decimale, come se fosse un numero intero, ma si dà a tutta la frazione decimale il nome dell’ultima cifra a destra.
Così sia da leggere il numero 5,238, si dirà cinque interi, poi si leggerà la parte decimale come numero intero dicendo: duecento trentotto millesimi, perchè l’ultima cifra a destra esprime millesimi.
ESERCIZI
SULLA NUMERAZIONE DECIMALE.
1° Si scrivano in cifre i seguenti numeri: tre interi più otto millesimi; zero metri e trecento venticinque millesimi di metro; venti mila e quattro lire e trecento otto millesimi; cinquantatre centesimi.
2° Leggansi i seguenti numeri: 34,255; 0,06; 0,3045; 804,003006.
3° Si dica quanti decimi ci vogliono per fare un intero; quanti centesimi per fare un decimo: quanti millesimi per fare un centesimo. Quanti centesimi vi sono in due interi; quanti millesimi in tre decimi. {26 [286]}
D. Come si fa l’addizione dei numeri decimali?
R. Si fa come quella dei numeri interi, badando solo di separare gì’interi dalle frazioni con una virgola; e quando dalla colonna delle frazioni si passa a quella delle unità, si portano le decine secondo il solito senza far conto che siano numeri interi o frazioni.
ESEMPIO: Un servo desideroso di dare un conto esatto al suo padrone ha notato la spesa nel modo seguente:
|
Speso in
formaggio
|
franchi
|
3,75
|
|
Speso in butirro
|
franchi
|
4,60
|
|
Speso in riso e
vermicelli
|
franchi
|
9,87
|
|
|
Totale franchi
|
18,22
|
Si dirà: 7 più 5 danno 12, si depone 2 e si prosegue: l più 8 danno 9, più 6 danno 15, più 7 fanno 22; deponiamo 2, dietro cui si scrive una virgola per separare le frazioni, indi si continua: 9 più 2 che si portano danno 11, più 4 danno 15, più 3 danno 18, totale 18, 22.
ESERCIZI.
1° Un signore desideroso di disporre bene delle sue ricchezze fa testamento e lascia per la ristorazione di una Chiesa L. 5500 e cent. 85. Per istruzione della gioventù fr. 580 cent. 60 annui. Ai poveri franchi 434 cent. 45. Quanto lascia in tutto?
2° Un padre facendo economia ha risparmiato in un anno fr. 825 cent. 90; suo figlio privandosi di parecchi divertimenti risparmiò franchi 226 cent. 32; la madre per sua special diligenza guadagnò fr. 167 cent. 42. Quanto hanno risparmiato tra tutti pel bene della famiglia?
3° Una madre per far lenzuola compera di tela metri 86, 17, per far camicie metri 62,9; per asciugamani metri 39,67. Quanti metri di tela ha comperato? {27 [287]}
D. Come si fa la sottrazione dei numeri decimali?
R. La sottrazione dei numeri decimali si fa come quella dei numeri interi, avvertendo solo di separare nel residuo gl’interi delle frazioni decimali con una virgola, la quale però deve sempre essere in colonna con quelle del minuendo e sittraendo.
Esempio:
|
Debbe pagare
|
341,28
|
|
Pago
|
141,17
|
|
Resta
|
200,11
|
Osservazione.- Se il
sottraendo ed il minuendo non avessero ugual di cifre nella frazione, si
suplisce con altrettanti zeri.
Esempio:
Debbe ricevere franchi 542 in due volte: ora riceve franchi 240 cent. 75. Quanto debbo ancora ricevere?
|
|
542, 00
|
aggiunti due 00
|
|
|
240,75
|
|
|
Resta
|
301,25
|
|
ESERCIZI.
1o Un lavorante deve ricevere in fine della settimana fr. 70, ma perchè ha perduto tempo, gli vengono ritenuti fr, 15, 50. Quanto porta ancora a casa?
2o Un operaio deve al panattiere franchi 200, 20; ha già pagato fr. 55, 65, ed ora ne paga 118, 15. Quanto dovrà ancora pagare?
3o Ho cpmperato 1425, 5 miriagrammi di uva peso brutto; sono da dimisuirsi 217 di tara, più 131 di consumo. Quanti miriagrammi restano ancora? {28 [288]}
D. Come si fa la moltiplicazione
dei decimali?
R. La moltiplicazione dei decimali si fa come quella dei numeri interi, notando solamente: 1o Quando vi sono delle frazioni si fa la moltiplicazione come se fossero tutti interi senza far caso della virgola. Nel prodotto poi si separano con una virgola tant cifre, quante erano le cifre frazionarie nei due fattori; 2o Per moltiplicare un numero decimale per dieci, per cento e per mille non si f altro che trasportare la virgola di una, due o tre cifre da sinistra a destra.
Esempio:
|
Ho comperato di
tela metri
|
120,50
|
|
Ogni metro pagato
|
3,45
|
|
Si moltiplica
|
60250
|
|
|
48200
|
|
|
36150
|
|
Addizione
|
415,7250
|
Le quattro cifre sarrano separate con una virgola, ed il prodotto sarà 415 fr. più 72 cent. Il resto sarebbe 50 diecimillesimi, i quali nel calcolo ordinario non si contano.
Osservazione. – Qualora non vi fossero tante cifre decimali nel prodotto quante separare colla virgola, si aggiungernno a sinistra del prodotto tanti 0 quanti bastano per completare le cifre decimali, più uno zero che tenga il luogo degli interi.
Per esempio: se il cacio si vendese fr. 0, 80 pr chilogramma quanto costranno chilogrammi 0,07?
Operazione:
|
Moltiplicando
|
0,07
|
|
Moltiplicatore
|
0,80
|
|
Prodotto fr.
|
0,0560
|
560 decimilessimi sarebbero il prezzo corrispondente ai sette centessimi di chilogramma. {29 [289]} Nel che si vede aggiunto uno 0 per completare le cifre dei fattori, ed un altro per tener luogo dell’unità.
2° Quanto costa una pezza di panno di metri 25, 55 a lire 10 al metro? Per risolvere il problema non si ha che da trasportare di un posto da sinistra a destra la virgola del moltiplicando: così si avrà per prodotto L. 255, 5.
ESERCIZI.
1° Quanto costano chilogrammi 343, 68 di pane a frane. 0,45 caduno?
2° Un giovane soleva ricevere dal padre pei suoi minuti piaceri ogni domenica fr, 1, 60; egli morigerato qual era, conservava tutto per comperarsi abiti, e darne parte ai poveri; quanto risparmio in un anno contando 52 domeniche all’anno?
3° Michele, ragazzo virtuoso, riceveva ogni giorno L. 0, 05 per comprarsi frutta: ogni mese dava 0, 50 in limosina, il resto lo spese a comprarsi buoni libri. Quanto diede in limosina? Quanto gli restò da spendere in libri?
D. Come si fa la divisione decimale?
R. La divisione decimale si fa come quella dei numeri interi, badando però alle seguenti avvertenze:
1° Quando il dividendo ed il divisore hanno egual numero di cifre dopo la virgola, la si toglie e si fa l’operazione come se fossero numeri interi, e nel quoziente saranno realmente interi.
2° Quando il dividendo od il divisore abbiano disugual numero di cifre nelle frazioni, lo si rende uguale con altrettanti 0 e si opera come sopra.
3° Quando si ha da dividere un numero decimale per 10, 100, 1000 ecc., basta trasportare la virgola di una, due, tre cifre da destra verso sinistra, {30 [290]}
ESEMPIO PEL 1°
CASO:
Ho speso fr. 678 cent. 75 in metri 45 e 25 centina, di stoffa; quanto mi costò ogni metro!
|
Dividendo
67875
|
4525 divisore
|
|
|
|
15 quozient
|
|
|
|
Osservazione. - Nel proposto esempio fa lo stesso che se uno avesse a dividere 67875 per 4525; il 15 (e sono 15 franchi) sarà il prezzo di ciascun metro.
ESEMPIO PEL 2° CASO;
Ho pagato fr. 115 cent. 50 per miriagrammi 5, 5 decimi di caffè; quanto mi costò cadun miriagramma? (5 decimi del miriagramma fanno 5 chilogrammi).
|
Dividendo
11550
|
550 divisore a
cui si aggiunge uno zero
|
|
|
|
21
|
|
|
|
Osservazione. - Si aggiunge uno zero, affinchè le cifre frazionali del divisore siano pari a quelle del dividendo, e, fatta secondo il solito la divisione, abbiam ottenuto per quoziente fr. 21 che è il prezzo di ciascun miriagramma.
N. B. Se nel dividendo soltanto vi fossero frazioni decimali, si potrebbe fare la divisione senza aggiungere i zeri al divisore; solo si deve avvertire di mettere una virgola nel quoziente quando si comincia a prendere una cifra decimale del dividendo, così per esempio 7, 26:3.
|
Dividendo
7,26
|
3 divisore
|
|
|
6
|
2,42
|
|
|
12
|
|
|
|
12
|
|
|
|
006
|
|
|
|
6
|
|
|
|
00
|
|
ESEMPIO PEL 3° CASO.
Carlo ha L. 343, 25 da distribuire fra 100 poveri, quanto toccherà a ciascuno?
Il dividendo 343, 25, divisore 100; il quoziente sarà L. 3, 4325. che si ottiene trasportando semplicemente la virgola di due cifre verso sinistra, {31 [291]}
D. Come si fa la divisione quando il dividendo è minore del divisore?
R. Si fa l’operazione secondo il solito, mettendo nno zero prima del quoziente per indicare che le cifre non esprimono numeri interi, e si aumenterà il dividendo di uno zero a destra se basta, altrimenti se ne aggiungeranno due, tre ecc. Anche basti, osservando però di mettere allora uno, due ecc. zeri dopo la virgola del quoziente.
ESEMPIO: - Come si dividono 6 franchi tra 15 persone?
Al dividendo si aggiunge uno 0; lo 0 aggiunto nel dividendo rende il numerodieci volte maggiore, ma il valore è sempre Io stesso, perchè queste nuove parti sonp dieci volte più piccole delle prime: vale a dire le unità coll’aggiunta di uno 0 diventano decimi; aggiungendone un altro avremo centesimi. Perciò nel dividendo invece di 60 decimi avremo 600 centesimi ed invece di 4 decimi nel quoziente avremo 40 centesimi.
D. Che cosa si deve fare quando in fine dell’operazione vi rimane un residuo minore del divisore?
R. A questo residuo si aggiunge uno 0 e si avranno decimi. Aggiunto poi un altro 0, si avranno centesimit e si continua la divisione. Ma quando si aggiunge uno 0 per avere i decimi od i centesimi allora bisogna tosto mettere una virgola nel quoziente per separare gli interi dalle frazioni.
ESEMPIO: - Si dividano franchi 20 a 3 operai
|
Dividendo
20
|
3 divisore
|
|
Si
sottrae
|
18
|
6,66
|
|
Per
ridurlo in decimi si aggiunge
|
20
|
|
|
Si
sottrae
|
18
|
|
|
Per
ridurlo in centesimi si aggiunge 0
|
20
|
|
|
Si
sottrae
|
18
|
|
|
|
2
|
|
Il quoziente sarà 6, 66. Il residuo 2 ( che sono centesimi) si potrebbe ridurre a millesimi coll’aggiunta di uno 0 e continuare la divisione, ma per lo più nel calcolo ordinario i millesimi si trascurano. {32 [292]}
ESERCIZI.
1o Un panattiere vende 800 miriagrammi di pane per settimana; quanti ne vende al giorno?
2o Un mugnaio ha esatto fr. 720, 75 per ettol. 28, 19 di frumento; quanto risulta per ciascun ettolitro?
3° Un mercante trova in cassa fr. 2345 per aver venduto di panno metri 200, 4; quanto ha esatto per ciascun metro?
D. Che cosa s’intende per Sistema metrico decimale?
R. Per Sistema metrico intendesi il complesso di tutti i pesi e di tutte le misure aventi il metro per base. Dicesi poi decimale perchè segue il sistema di numerazione decimale.
D. Che cosa è il metro e quale ne è la lunghezza?
R. Il metro è la diecimilionesima parte del quarto del meridiano terrestre, ossia della circonferenza della terra.
Vale a dire, se intorno alla terra si tirasse un filo e che questo Alo si dividesse in quaranta milioni di parti uguali, una parte formerebbe la lunghezza del metro.
D. Che cosa vuol dire metro?
R. La parola metro significa misura.
D. Perchè preferire questo sistema all’antico che già si aveva in uso?
R. Perchè rende molto più facile il calcolo: ma quello
che è più essendo
il metro eguale in tutte le parti {33 [293]} del mondo, si eviterà la grande
varietà di pesi e misure che occorrono talvolta nello stesso Stato e spesso
nella medesima provincia. Per questa diversità di pesi e di misure uno va
esposto ad errori ed inganni di ogni genere. Il che di leggieri si potrà
evitare in quei luoghi in cui si farà uso del nuovo sistema.
D. Quali sono le unità fondamentali del sistema metrico decimale?
R. Le unità fondamentali di questo sistema sono sei:
Il metro per le misure di lunghezza.
Il metro quadrato per la superficie.
Lo stero o metro cubo pei volumi.
Il litro per le misure di capacità, come vino, acqua, grano, meliga e simili.
Il gramma per li pesi.
Il franco o lira nuora per le monete.
D. In quali misure si userà il metro?
R. Il metro si userà in tutte le misure di lunghezza, come sono tela, panno, strade e simili.
D. Per misurare il pavimento, le pareti di una casa, i campi, i prati e le vigne si userà anche il metro?
R. Per misurare le superficie si usa il metro quadrato, che è una superficie di quattro lati, ciascuno dei quali è lungo un metro. Ma siccome questa misura sarebbe troppo piccola per le campagne, cosi in luogo del metro quadrato venne adottato il decametro quadrato, che è una superficie di quattro lati ciascuno dei quali è lungo dieci metri.
D. Qual nome si dà al decametro quadrato?
R. Il decametro quadrato venne detto ara. {34 [294]}
D. Che cosa è lo stero e quale ne à l’uso?
R. Lo stero è un metro cubo, cioè un corpo che ha un metro di spigolo, ossia un metro in altezza, lunghezza e larghezza. Questa misura però ha una forma diversa dal metro cubo che è fatto come un dado per renderlo adatto ad usarsi pel fieno, paglia, legna ghiaia e simili.
D. Che cosa è il litro?
R. Il litro è un decimetro cubo. Per farcene un’idea supponiamo il metro lineare diviso in dieci parti uguali, e avremo un decimetro ossia la decima parte del metro. Ora un decimetro cubo, ossia un vaso lungo, largo, alto un decimetro forma la capacità del litro. Esso si usa per le misure di capacita, cioè pei liquidi, come olio, vino, birra ecc. e per le materie secche come frumento, riso, castagne, ceci, fave ecc.
D. Che cosa s’intende per gramma?
R. Un gramma è il peso dell’acqua distillata contenuta in un centimetro cubo. Se si prende il metro lineare e si divide in cento parti uguali; ciascuna di queste parti dicesi centimetro. Dicesi centimetro cubo un vaso lungo, largo, alto un centimetro. Il gramma serve per le misure di peso.
D. Che cosa s’intende per un franco ossia lira nuova?
R. S’intende una moneta d’argento del peso di cinque grammi. Esso si usa per le misure di valore, cioè per determinare il prezzo di un oggetto, di un lavoro ecc.
D. Come si può dimostrare che tutte le misure derivano dal metro?
R. Il metro essendo la base di tutte le misure decimali, tutte le altre devono da quello derivare.
L’ara ossia il decametro quadrato è un quadrato i cui lati hanno dieci metri di lunghezza.
Lo stero o metro cubo è uguale ad un dado che {35 [295]} abbia un metro di spigolo: vale a dire un metro in lunghezza, larghezza e profondità.
Il litro origina dal metro essendo la capacità di un decimetro cubo.
Il gramma viene altresì dal metro, giacchè è il peso di un centimetro cubo d’acqua pura e distillata.
Il franco risulta anche dal metro, giacchè pesa cinque grammi.
D. Che cosa intendesi per multiplo decimale?
R. Per multiplo decimale intendesi una delle suddette unità resa di dieci in dieci volte maggiore.
Per es. 1 moltiplicato per 10 dà 10. Questo dieci dicesi Deca: 10 moltiplicato per 10 dà 100, che dicesi Etto.
D. Che cosa intendesi per sottomultiplo?
R. Per sottomultiplo intendesi l’unità resa di dieci in dieci volte minore.
Per es. 1 diviso per 10 darà uà decimò dell’unità che dicesi Deci.
D. Quanti sono i multipli?
R. I multipli ossia le voci che servono ad esprimere l’aumento sono quattro, espresse colle seguenti parole greche: Deca che vuol dire dieci unità; Etto che vuol dire cento; Kilo che vuol dire mille; Miria che vuol dire dieci mila.
D. Quanti sono i sottomultipli?
R. I sottomultipli, ossia le voci che servono ad esprimere le parti dell’unità, sono tre: deci che vuol dire la decima parte dell’unità, centi, la centesima; milli, la millesima.
D. Che differenza passa tra deca e deci?
R. Deca vuol dire dieci unità, deci, la decima parte della medesima unità. {36 [296]}
D. Come si possono applicare i multipli alle unità fondamentali?
R. Se a Deca, Etto, Kilo, Miria, aggiungo metro, avrò Decametro, Ettometro, Eliometro, Miriametro. Lo stesso facciasi delle altre unità.
D. Come si possono applicare i sottomultipli?
R. Se alle voci deci, centi, milli, aggiungo metro, avrò decimetro, centimetro, millimetro, ossia la decima, la centesima, la millesima parte del metro.
Il seguente specchio servirà a dilucidare quanto si è detto di sopra.
|
Appellazione
scritta
|
In cifre
|
In decimali
|
|
Unità
|
1
|
Unità
|
|
Decina
|
10
|
Deca
|
|
Centinaio
|
100
|
Etto
|
|
Mille
|
1000
|
Chilo
|
|
Decina di mila
|
10000
|
Miria
|
|
Centinaio di mila
|
100000
|
Deca-Miria
|
|
Milione
|
1000000
|
Etto Miria
|
Qualora trattisi di pesi il deca-miria dioesi quintale e l’ettomiria si suol appellare tonnellata.
Dal che risulta che una cifra diventa di dieci in dieci volte maggiore a misura che si avanza di una sede verso sinistra. All’opposto ogni volta che una cifra si avanza di una sede Verso la destra, diventa di dieci in dieci volte più piccola, come:
|
Unità
|
1
|
unità
|
|
Decimo
|
0,1
|
deci, decima
parte dell’unità
|
|
Centesimo
|
0,01
|
centi,centesima,parte
dell’unità
|
|
Millesimo
|
0,001
|
milli, millesima
p
|
|
Diecimilli
|
0,0001
|
decimilli, decimillesima
p
|
|
Centimillì
|
0,00001
|
centimilli;
centomillesima p.
|
|
Milionesimo
|
0,000001
|
millimilli,
milionesima p {37 [297]}
|
D. I numeri esprimenti misure decimali si scrivono e si leggono sempre secondo le regole dei numeri decimali?
R. Si, per regola generale si scrivono e si leggono secondo le regole pei numeri decimali; devesi solo notare:
1° Che talvolta si prende come unita di misura ciò che è multiplo della vera misura; ed in tal caso dietro a questo multiplo scrivasi subito la virgola, e i numeri che vengono in seguito saranno considerati come suoi sottomultipli o frazioni decimali. Così sebbene pei pesi la vera unità di misura sia il gramma, tuttavia sovente si considera come unità il kilogramma. Se per esempio si avesse da scrivere chilogrammi quattro, e vent’otto decagrammi. In questo numero i chilogrammi sono considerati come unità di misura e si scriverà dopo il 4 la virgola, e dopo questa parte l’altra parte del numero decimale in questo modo: 4, 28.
2° Devesi pur notare che per le misure di superficie ciascun multiplo o sottomultiplo o unità vale cento volte il multiplo o sottomultiplo dell’unità immediatamente inferiore. Così un decàmetro quadrato vale cento metri quadrati, un metro quadrato vale cento decimetri quadrati, un decimetro quadrato vale cento centimetri quadrati; perciò nello scriverli ci vogliono due cifre per ciascun sottomultiplo, una per le decine l’altra per le unità, e si supplisce con {38 [298]} seri quando vi manchino le unità o le decine. Cosi per iscrivere due metri quadrati, e tre decimetri si scriverà 2, 03, mettendo lo zero per supplire alle decine mancanti nei decimetri quadrati.
Che se vi fosse a scrivere quattrocento metri quadrati e duecento sessanta centimetri quadrati, si scriverà 400, 0260, il primo zero per supplire le decine dei decimetri quadrati, ed un altro zero per supplire le unità dei centimetri quadrati.
Se poi si tratta di leggere tali numeri, si dividono le cifre a destra della virgola di due in due da sinistra a destra; poscia si leggerà tutta la frazione decimale come numero intero dandole il nome dell’ultima casella a destra. Sia a leggere il numero Etm. q. 28, 5626; siccome qui l’unità di misura sarebbero gli ettometri quadrati, le due prime cifre dopo la virgola saranno decametri quadrati e le due ultime metri quadrati, e si dirà 28 ettometri e cinquemila seicento ventisei metri quadrati.
3° Finalmente devesi notare che nelle misure cubiche ciascun’unità, o multiplo, o sottomultiplo vale mille volte l’unità, o multiplo, o sottomultiplo immediatamente inferiore; perciò ci vorranno tre cifre per esprimere i decimi, cioè unità, decine e centinaia di decimi, tre cifre per esprimere i centesimi, ecc. e si supplirà con zeri alle unità, decine e centinaia mancanti; mentre per leggere tali numeri si dividono le cifre della parte frazionaria di tre in tre da sinistra verso destra, le tre prime dopo la virgola esprimeranno i decimi cubi, le tre altre i centesimi cubi; e leggendo come numero intero si darà a tutta {39 [299]} la frazione il nome dell’ultima casella. Sia dà scriversi il numero quattro metri cubi e trentasei decimetri cubi; si scriverà 4, 036 mettendo lo zero, perchè mancano le centinaia di decimetri cubi. Sia da leggersi il numero m. c. 8, 367608 si comincieranno a dividere le cifre della frazione decimale di tre in tre: e così si troveranno tre cifre pei decimetri cubi, e tre pei centimetri cubi, e si dirà metri cubi 8 e trecento sessantasette mila seicento otto centimetri cubi.
D. Ciascuna delle unità fondamentali ha tutti i multipli e sottomultipli?
R. Il metro, il litro, il gramma hanno tutti i quattro multipli, e tutti i tre sottomultipli. Ma l’ara, ha un solo multiplo che è l’ettara (100 are) ed un solo sottomultiplo, che è il centiara (centesima parte dell’ara). Lo stero ha il solo decastero ed il decistero.
D. Quali abbreviazioni soglionsi usare nel sistema metrico decimale?
R. Per regola generale vuoisi esprimere l’unità di misura colla sua lettera iniziale minuscola. Così per iscrivere metri 6, grammi 15, ecc. si scriverà semplicemente m. 6, g. 15. Per esprimere i multipli, a sinistra della lettera suddetta, si scrive maiuscola la lettera iniziale del multiplo; si scriverà poi minuscola la lettera iniziale del sottomultiplo, quando si abbia da scrivere un sottomultiplo. Così per abbreviare le espressioni: due decalitri si scriverà Dl. 2; per abbreviare l’espressione 44 centigramma si potrà scrivere cg. 44. Così pure Kg. 36, 75; Em. 5, 26, Dl. 7, 5 si leggerà Chilogrammi 36 e 75 decagrammi; Ettometri 5 e 26 metri; Decalitri 7 e 5 litri. {40 [300]}
D. Che cosa s’intende per frazioni ordinarie?
R. Le frazioni ordinarie sono quelle che esprimono le parti dell’unità in qualunque modo questa sia divisa.
Come cinque ottavi di un foglio, tre quarti della terra. la
metà di una noce.
D. Con quali numeri si suole esprimere una frazione?
R. Una frazione si suole esprimere con due numeri chiamati numeratore e denominatore. Il denominatore indica in quante parti è divisa l’unità, il numeratore indica quante si prendono di queste parti.
D. Come si pronunciano il numeratore ed il denominatore?
R. Il numeratore si pronuncia enunciando il numero che lo rappresenta tal quale è scritto; e si dirà uno, due, tre, dieci, venticinque ecc. Nel denominatore i numeri due, tre, quattro, ecc. sino al dieci si dicono metà, terzi, quarti, quinti, sesti, settimi, ottavi, noni, decimi; oltre il dieci si pronuncierà il numero aggiungendo alla penultima lettera la terminazione esimo. Così noi diremo: tre undicesimi, quattordici quarantacinquesimi.
D. Come si scrivono le frazioni?
R. Mettendo il numeratore sopra il denominatore separati fra loro con una linea orizontale o traversale come
oppure anche ¾.
D. Come si suddividono le frazioni ordinarie?
R. Le frazioni si suddividono in proprie ed in improprie. Le frazioni proprie sono quelle che esprimono un numero minore dell’unità, come ½ , 4⁄7; queste hanno i numeratore minore del denominatore. Le frazioni improprie sono quelle che avendo il {41 [301]} numeratore più grande del denominatore non contengono solo delle parti dell’unità o solo unità intere, ma uniti e parti di unita, come 17/5, 26/6. Diconsi apparenti quelle che banno i due termini eguali, oppure un numeratore che è multiplo del denominatore, cioè il doppio o il triplo ecc.; come 3/3 8/2. Queste frazioni sebbene sieno scritte sotto forma di frazione equivalgono ad unità intere. Infatti 3/3 equivale ad un’unità; 8/2 equivale a quattro unità. Dicesi numero misto quello composto di unità e di frazioni.
Così per esempio 3 2/5; 513/15 sono numeri misti.
D. Come si spezza una frazione impropria, cioè come si possono separare in una frazione impropria gl’interi dalla parte frazionaria?
R. Dividendo il numeratore pel denominatore. Il quoziente esprimerà gli interi, il residuo sarà il numeratore della parte frazionaria, mentre il divisore continuerà ad essere il denominatore.
Così per estrarre le unità da 17/5 si divide il
17 per 5
Il quoziente 3 indicherà le unità,
il residuo 2 sarà il numeratore ed il divisore 5 il denominatore della nuova
frazione, quindi avremo 17/5 = 32/5
D. Come si riduce un numero intero in frazione, cioè in terzi, in quarti, in undicesimi ecc.
R. Moltiplicando il numero intero pel denominatore che gli si vuol dare, cioè se si vuol ridurre in terzi si moltiplicherà per 3; se in quarti si moltiplicherà per {42 [302]} 4, se in undicesimi per li ecc., e al prodotto si darà per denominatore questo numero.
Così se si vuol ridurre 5 interi in sesti, si moltiplica 5 per 6 e si dà per denominatore lo stesso sei, quindi si avrà 5 = 30/6.
D. Come si può ridurre un numero composto di interi e frazioni ad una sola frazione?
R. Moltiplicando il denominatore per gli interi ed aggiungendo al prodotto il numeratore, lasciando lo stesso denominatore.
Così per ridurre in una sola frazione 3 interi e due quinti, si moltiplica il 5 per 3, al prodotto 15 si aggiunge il numeratore 2, e così si avrà 3 2/5 = 17/5.
D. A quale mutazione va soggetta una frazione se si moltiplica uno solo de' suoi termini?
R. Se si moltiplica solo il suo numeratore, la frazione resta moltiplicata, così data la frazione 2/3 se io moltiplico il numeratore due per quattro, avrò 8/3, che è una frazione 4 volte più grande che 2/3; se all’opposto moltiplico il solo denominatore, la frazione resta divisa. Cosi nella frazione proposta 2/3, se moltiplico il denominatore 3 per 4 avrò 2/12 che è quattro volte più piccola che 2/3 giacchè il denominatore 12 indica che l’unità fu divisa in parti 4 volte più piccole.
D. Che cambiamento fa una frazione, di cui si divida un solo termine?
R. Essa cambia secondo il termine che si divide. Dividendo il numeratore la frazione resta divisa, così in 6/8 dividendo il numeratore 6 per 2 avrò 3/8 che è frazione due volte più piccola che 6/8. All’opposto dividendo il suo denominatore, la frazione resta moltiplicata, così in 6/8 dividendo il denominatore 8 per 2 avrò 6/4 che è una frazione due volte più grande che 6/8, giacchè le parti in cui è divisa {43 [303]} l’unità, diventano più grandi; infatti i quarti sono il doppio degli ottavi.
D. Che cambiamento fa una frazione moltiplicando o dividendo i due termini per lo stesso numero?
R. La frazione non cambia di valore.
Così per es. moltiplicando per 2 i due termini della frazione 1/2 avremo 2⁄4 che è perfettamente eguale ad una metà: Così pure dividendo i termini della frazione 4/8 per quattro avremo 1⁄2 che è perfettamente uguale a 4/8.
Dal che si vede che moltiplicando o dividendo i termini di una frazione per lo stesso numero la frazione non cambia valore, ma si trasforma in altra equivalente.
D. Non si potrebbe ridurre una frazione ordinaria in frazione decimale?
R. Si può ridurre una trazione ordinaria in decimale dividendo il numeratore pel denominatore. Quando il denominatore non sia contenuto nel numeratore si porrà nel quoziente uno zero seguito da una virgola e si aggiungerà pure al dividendo uno zero, e così si continuerà la divisione secondo le regole date superiormente; le cifre che si otterranno nel quoziente saranno frazioni decimali.
Sia da ridurre la frazione ordinaria 3/4 in frazione decimale.
Così facendo, si otterranno molte volte frazioni decimali equivalenti alle ordinarie, ed altre volte non si potranno avere tali frazioni decimali perfettamente equivalenti, ma si otterranno, frazioni decimali con valore tanto più approssimato, quanto più si continuerà la divisione. {44 [304]}
D. Che cosà vuol dire ridurre una frazione ai minimi termini?
R. Vuol dire rendere i suoi termini più piccoli che si può, ossia ridurli alla più semplice espressione.
D. Come si riduce una frazione alla più semplice espressione?
R. Per ridurre una frazione alla più semplice espressione, si comincia a vedere se i suoi due termini sono divisibili per uno stesso numero, di poi si dividono per questo stesso numero finchè si può, poscia si passa a dividerli per un altro numero finchè si può, e così di seguito finchè i due termini non hanno più un divisore che possa dividerli tutti e due, cioè un divisore comune.
PER ESEMPIO;
44 |
22 |
2 |
54 |
27 |
9 |
46 |
23 |
-------- |
= |
------- |
= |
------ |
------- |
= |
------- |
= |
------ |
------- |
= |
------- |
66 |
33 |
3 |
96 |
48 |
16 |
72 |
36 |
D. Come si chiama quella frazione i cui termini non hanno divisore comune?
R. Si chiama irreduttibile.
ESEMPIO: La frazione 14/57 è irreduttibile perchè il valore di 14⁄27, non può esprimersi con cifre più piccole.
D. Non vi è alcun altro mezzo per ridurre le frazioni a minimi termini?
R. Quando non si trova a prima vista un divisore comune ài due termini si ricorre alla ricerca del massimo comun divisore. {45 [305]}
D. Che cosa e il massimo oomun divisore?
R. Il M. G. D. è il numero più grande che divida esattamente i due termini di una frazione.
D. Come si fa per trovare il M. G. D. di una frazione?
R. Proposta una fazione, si divide il termine maggiore pel minore, il quoziente si scrive sopra il divisore, ed il resto, se vi è, diventa divisore del primo divisore, e perciò si scrive alla sua destra. Il nuovo quoziente si scrive sopra il nuovo divisore, ed il resto diventa divisore di questo secondo divisore; e cosi si proseguisce finchè si trovi un divisore il quale divida il suo dividendo esattamente. Questo numero è il M. G. D. ESEMPIO:
D. A che cosa serve il M. G. D.?
R. Siccome esso divide esattamente i due termini di una frazione, così serve a ridurre prontamente la frazione a minimi termini. Infatti nell’esempio precedente.
143:13 = 11 e 637:113 = 49 perciò
D. Che cosa vuol dire ridurre una o più frazioni allo stesso denominatore?
R. Vuol dire fare in modo che due o più frazioni vengano ad avere lo stesso denominatore senza che cambino di valore. {46 [306]} Come sì fa per ridurre le frazioni allo stesso denominatore?
R. Si moltiplicano i due termini di ciascuna frazione pel prodotto dei denominatori di tutte le altre.
ESEMPIO:
|
2
|
,
|
4
|
,
|
3
|
,
|
40
|
,
|
48
|
,
|
45
|
|
3
|
5
|
4
|
60
|
80
|
60
|
D. Su qual principio si appoggia questa riduzione allo stesso denominatore?
R. Sul principio che moltiplicando i due termini di una frazione per uno stesso numero, questa frazione non cangia di valore; infatti noi non facciamo altro che moltiplicare i due termini di ciascuna per uno stesso numero cioè, pel prodotto dei denominatori delle altre.
D. Non vi e altro modo di ridurre allo stesso denom.?
R. Può accadere alcune volte che proposte più frazioni da ridursi, ve ne sia una il cui denominatore sia multiplo dei denom. di tutte le altre; ed in tal caso questo denom. resta il denom. comune, e per ottenere il numeratore di ciascuna frazione si divide il denom. comune pel denom. di ciascuna frazione. Il quoziente poi si moltiplica pel numeratore della frazione corrispondente. Il prodotto ne sarà il numeratore.
ESEMPIO:
1 |
5 |
10 |
8 |
20 |
2 |
- |
- |
- |
- |
- |
- |
36 |
7 |
3 |
2 |
1 |
14 |
40 |
8 |
4 |
5 |
2 |
20 |
- |
- |
- |
- |
- |
- |
36 |
35 |
30 |
16 |
20 |
28 |
40 |
40 |
40 |
40 |
40 |
40 |
D. Qual cangiamento fa una frazione qualora si aggiunga o si tolga uno stesso numero ai suoi due termini?
R. Se questa frazione è propria aumenta o diminuisce {47 [307]} di valore secondochè si aggiunge o si toglie, se è impropria allora diminuisce aggiungendo, ed aumenta col togliere una medesima quantità ai due termini.
D. Quanti casi presenta l’addizione delle frazioni?
R. Due casi: 1° L’addizione delle frazioni proprie ed improprie; 2° delle frazioni miste o numeri frazionari.
D. Come si fa l’addizione nel l°caso?
R. Proposte due 0 più frazioni per farne l’addizione si devono ridurre prima di tutto allo stesso denominatore, se ancor non lo sono, poscia si fa l’addizione dei numeratori dando al totale il comun denominatore. Se la frazione risultante è impropria, se ne possono estrarre gli interi nel modo sopra accennato.
ESEMPIO:
|
2
|
+
|
4
|
+
|
1
|
=
|
20
|
+
|
24
|
+
|
15
|
=
|
59
|
=
|
29
|
|
3
|
5
|
2
|
30
|
30
|
30
|
30
|
30
|
D. Come si fa l’addizione nel 2° caso?
R. Prima di tutto si fa l’addizione delle frazioni proprie nel modo indicato, se la frazione risultante è impropria, se ne estraggono gli interi; poscia si fa l’addizione di tutti gli interi.
ESEMPIO:
|
2
|
+
|
1
|
+
|
1
|
+
|
2
|
+
|
8
|
+
|
9
|
=
|
(2+1+8)
|
+ (
|
1
|
+
|
2
|
+
|
9
|
)=
|
11+
|
17
|
=12
|
5
|
|
3
|
6
|
12
|
3
|
6
|
12
|
12
|
12
|
ESERCIZI.
1o Eseguire le addizioni seguenti:
|
35
|
+
|
15
|
+
|
25
|
;
|
12
|
+
|
9
|
;
|
7
|
+
|
3
|
;
|
1
|
+
|
3
|
+
|
2
|
|
75
|
75
|
75
|
28
|
14
|
13
|
7
|
12
|
4
|
3
|
{48 [308]}
2° Un povero, contento dell’elemosina ricevuta, fa i suoi conti.
Al mattino prese 9⁄20
più 2/10 di lira. Alla sera 1⁄5 più 10⁄25
di lira. Quanto ha preso tutto quel giorno?
3° In un recipiente si vuotarono successivamente litri 5 e 3/5 di acqua, quindi litri 4 e 11/12 e per ultimo litri 3 e 3/2 e fu colmo. Quanta acqua contiene quel recipiente?
D. La sottrazione delle frazioni quanti casi presenta?
R. Presenta tre casi: 1° sottrazione di una frazione da un intero; 2° sottrazione di una frazione semplice da un’altra semplice; 3° sottrazione di frazioni miste.
D. Come si fa la sottrazione nel primo caso?
R. Nel primo caso si riducono gli intieri alla forma di frazione col denominatore della frazione data, quindi si fa la sottrazione dei numeratori dando lo stesso denominatore al residuo, e si avrà così una frazione da cui si potranno di nuovo estrarre gli intieri.
ESEMPIO:
|
3
|
-
|
2
|
=
|
9
|
-
|
2
|
=
|
7
|
=
|
2
|
+
|
1
|
|
3
|
3
|
3
|
3
|
3
|
D. Come si fa la sottrazione nel secondo caso, cioè quando si deve togliere una frazione semplice da un’altra semplice?
R. Si devono ridurre le due frazioni allo stesso denominatore, se non lo sono, quindi fare la sottrazione dei numeratori dando al residuo lo stesso denominatore.
ESEMPIO:
|
3
|
-
|
2
|
=
|
9
|
-
|
8
|
=
|
1
|
|
4
|
3
|
12
|
12
|
12
|
D. Come si fa la sottrazione delle frazioni nel terzo caso, quando cioè vi sono dei numeri frazionari?
R. Si riducono i numeri frazionari in frazioni improprie, quindi si riducono allo stesso denominatore, e si fa {49 [309]} la sottrazione nel modo indicato. Se il residuo è una frazione impropria se ne estraggono gl’interi.
ESEMPIO:
|
3
|
2
|
-
|
2
|
8
|
=
|
23
|
-
|
26
|
=
|
207
|
-
|
182
|
=
|
25
|
|
7
|
9
|
7
|
9
|
63
|
63
|
63
|
ESERCIZI.
1° Si eseguiscano le sottrazioni:
|
25
|
-
|
21
|
;
|
4
|
-
|
3
|
;
|
25
|
-
|
7
|
;
|
5
|
2
|
-
|
3
|
2
|
|
36
|
36
|
5
|
4
|
50
|
15
|
7
|
3
|
2o Un mercante vendette 3/7 di una pezza di panno; quanto di quella pezza gliene rimase?
3° Un viandante ha percorso 1⁄3 più 1⁄8 più 2⁄5 del suo cammino; quanto gliene rimane a fare?
4° Si comperarono m. 25 1⁄2 di panno. Se ne vendettero m. 7 e 3/4• Quanti ne rimangono?
D. Quanti casi di moltiplicazioni delle frazioni vi sono?
R. Tre casi: 1° moltiplicazione di un intero per una frazione e viceversa; 2° moltiplicazione di frazioni semplici; 3° moltiplicazione di numeri frazionari.
D. Come si fa la moltiplicazione nel primo caso?
R. Si moltiplica l’intero pel numeratore e al prodotto si dà lo stesso denominatore.
ESEMPIO:
D. Come si fa la moltiplicazione nel secondo caso?
R. La moltiplicazione nel secondo caso si fa moltiplicandone i numeratori fra di loro, ed i denominatori fra loro.
ESEMPIO:
{50 [310]}
D. Come si fa la moltiplicazione nel terzo caso?
R. Per moltiplicare due numeri frazionari prima si debbono ridurre in frazioni improprie e poscia eseguire la moltiplicazione nel modo sopraccennato.
ESEMPIO
|
2
|
1
|
x
|
5
|
2
|
=
|
5
|
x
|
17
|
=
|
85
|
=
|
14
|
+
|
1
|
|
2
|
3
|
2
|
3
|
6
|
6
|
ESERCIZI.
1° Si eseguiscano le seguenti moltiplicazioni:
|
35
|
x
|
10
|
;
|
25
|
x
|
9
|
;
|
3
|
x
|
2
|
x
|
3
|
;
|
1
|
x5
|
+
|
4
|
|
60
|
37
|
4
|
5
|
7
|
2
|
7
|
Trovare i 2⁄3 di 4/5 di 1/2 della somma di lire 300.
2° Enrico sa di fare la 1/2 del suo viaggio in un’ora; dopo 3/4 d’ora quanto ne ha fatto?
3° Qual’è il numero di cui i 5⁄6 degli 8/9 fanno L. 20?
D. Quanti casi devonsi distinguere nella divisione delle frazioni?
R. Tre: 1° Divisione di un numero intero per una frazione e viceversa; 2° divisione di una frazione semplice per un’altra semplice; 3° divisione di frazioni fra cui ve ne siano delle miste.
D. Come si eseguisce la divisione nel primo caso?
R. Per dividere un intero per una frazione si dà all’intero per denominatore l’unità, quindi si capovolge la frazione, poscia si fa la moltiplicazione.
ESEMPIO:
|
3
|
:
|
2
|
=
|
3
|
x
|
5
|
=
|
15
|
=
|
7
|
+
|
1
|
|
5
|
1
|
2
|
2
|
2
|
{51 [311]}
Viceversa, per dividere una frazione per un intero, si moltiplica il denominatore per l’intero e si lascia lo stesso numeratore.
ESEMPIO:
D. Come si fa la divisione nel secondo caso?
R. Per dividere una frazione per un’altra bisogna capovolgere la frazione divisore, quindi si fa la moltiplicazione.
ESEMPIO:
|
3
|
:
|
2
|
=
|
3
|
x
|
4
|
=
|
12
|
=
|
6
|
|
7
|
4
|
7
|
2
|
14
|
7
|
D. Come si fa la divisione nel terzo caso?
R. Per eseguire una divisione in cui vi siano delle frazioni miste, primieramente è necessario ridurre le frazioni miste in improprie, poscia capovolgere la frazione divisore, e quindi fare la moltiplicazione.
ESEMPIO:
|
3
|
1
|
:
|
2
|
1
|
=
|
7
|
:
|
9
|
=
|
7
|
x
|
4
|
=
|
28
|
=
|
14
|
=
|
1
|
5
|
|
2
|
4
|
2
|
4
|
2
|
9
|
18
|
9
|
9
|
ESERCIZI.
1° Si eseguiscano le divisioni seguenti:
|
75
|
:6
|
;
|
5
|
:3
|
;
|
8:
|
4
|
;
|
3:
|
5
|
;
|
7
|
:
|
5
|
;
|
8
|
:
|
6
|
;
|
125
|
:
|
3
|
|
120
|
4
|
5
|
6
|
2
|
6
|
15
|
15
|
720
|
4
|
2° In 3/4 d’ora un corriere percorse 6 chilometri: in quale tempo avrà percorso un chilometro?
3° Tizio vendette la sua casa a L. 4568 ma coll’aumento dei 2⁄20 di quanto costava ad esso: quanto gli era costata?
4° In 3/4 d’ora si fecero 3⁄8 di un lavoro; si chiede quanto se ne farebbe in un’ora? {52 [312]}
D. Quali sono i numeri complessi?
R. Numeri complessi diconsi quelli che sono composti di più parti, le quali vanno a riferirsi rispettivamente a più suddivisioni di una stessa unità, p. e. 4 trabucchi, 2 piedi, 3 oncie; nibbi 4, libbre 7, oncie 8; lire 2, soldi 11, denari 7, sono numeri complessi.
D. Qual è la prima operazione, che si deve fare per ridurre un numero complesso in frazione decimale?
R. La prima operazione si è di ridurre il numero complesso in frazione ordinaria della unità principale.
D. Che vuol dire ridurre un numero complesso in frazione ordinaria dell’unità principale?
R. Vuol dire ridurre tutto il numero complesso all’ultima suddivisione in esso espressa e dar poscia al numero risultante per denominatore l’unità dello stesso genere ridotta alla ultima suddivisione espressa dal numero complesso.
ESEMPIO:
|
Trab.
|
Piedi
|
Oncie
|
|
3.
|
4.
|
9.
|
Si cominciano ridurre i trabucchi in piedi; ogni trab. vale 6 piedi; e però 3 trab. valgono 18 piedi: a questi 18 aggiungendo i 4 piedi che abbiamo, faranno 22. Ora i 22 piedi devonsi ridurre in oncie; ogni piede vale 12 oncie; e 22 piedi valgono 264 oncie, cui aggiugnendo le 9 oncie che già abbiamo, risultano 273 oncie. Questo numero sarà il numeratore. Per avere il denominatore riduciamo 1 trabucco in piedi e ne avremo 6; ì 6 piedi in oncie e ne avremo 72; così si avrà il numero complesso eguale alla frazione ordinaria di trabucco.
|
Tr.
3, p. 4, on. 9
|
=
|
273
|
|
72
|
{53 [313]}
D. Che si deve fare di più per ridurre il numero complesso in frazione decimale?
R. Ottenuta nel modo sopraccennato una frazione ordinaria, non si ha più che a ridurre la frazione ordinaria in frazione decimale nel modo già altre volte indicato, cioè dividendo il numeratore pel denominatore.
Così:
|
Tr.
3, p. 4, on. 9
|
=
|
273
|
= 273
: 72 = 3, 7916
|
|
72
|
D. Come si fa per ridurre una frazione decimale in un numero complesso?
R. Per ridurre una frazione decimale in un numero complesso, bisogna ridurre questa frazione decimale in frazione ordinaria, poscia dividere il numeratore pel denom. e quando non si hanno più cifre da abbassare, moltiplicare il resto, se vi è, per la prima suddivisione del numero complesso in cui si vuole ridurre, e dividere nuovamente il prodotto per lo stesso dividendo; poscia se ancor vi sarà qualche resto moltiplicarlo per la seconda suddivisione, e così di seguito. Bisogna però nel quoziente separare gli interi dalle unità della prima suddivisione, queste unità da quelle della seconda suddivisione ecc.
Così abbiasi da ridurre L. 3,47 in numero complesso. Anzi tutto riduco questo numero decimale in frazione ordinaria ed avrò 347⁄100. Ciò fatto divido il numeratore pel
|
Lire
|
Soldi
|
Danari.
|
|
3
|
9
|
4.
|
Dal che si vede che non sempre si può ridurre un numero decimale in un numero complesso perfettamente eguale, ma bisognerà talvolta contentarsi di un numero approssimativo.
D. Che cosa s’intende per regola del tre?
R. S’intende il modo di risolvere i problemi, in cui, dati tre numeri, se ne cerca un quarto che abbia con uno di essi la stessa relazione, che hanno gli altri due fra loro.
Per es. 3 operai fanno 12 metri di lavoro in un giorno, si ‘cerca quanti ne faranno in un giorno 7 operai. Come si vede qui abbiamo tre numeri, e se ne cerca un quarto, cioè il numero dei metri che faranno 7 operai, si cerca cioè un numero che sia in relazione col numero 7 operai, come il numero 12 dei metri è in relazione col numero 3 operai.
D. In quanti casi può accadere di aver bisogno di tal regola?
R. In due casi: 1° Quando, dato il valore di un determinato numero di unità, si cerca il valore di un altro determinato numero.
Così per es. 3 operai fanno in un giorno 12 metri di lavoro, 7 operai quanti ne faranno? In questo problema si ha il valore di un determinato numero di operai, si sa cioè che tre operai valgono a fare 12 metri, e si cerca il valore di un altro determinato numero di operai, cioè quanti metri valgono a fare 7 operai. {55 [315]} 2° Quando, dato un numero determinato di unità ed il valore di ciascuna, si cerca quante unità si potranno avere colla stessa somma, ma cambiando il valore dell’unità in altro determinato valore.
Cosi per es. Con una somma potrei comperare 9 metri di stoffa a lire 6 al metro, quanti ne potrò comperare colla stessa somma a L. 18 al metro?
D. Quale regola tenere per risolvere i problemi che si riferiscono al primo caso?
R. Nel primo caso conoscendosi il valore di un determinato numero di unità, si deve primieramente cercare il valore di un’unità col dividere il valore di tutte pel numero delle unità. Il quoziente indicherà il valore di ciascuna. Poscia si moltiplicherà questo quoziente pe l’altro numero di unità, di cui si cerca il valore.
Così nel proposto esempio si divide il numero 12 per 3 e si avrà per quoziente 4 che indica il lavoro di un operaio. Con questo quoziente 4 moltiplicherò l’altro numero di operai, cioè il 7, giacchè è chiaro che 7 operai faranno 7 volte 4 metri, e così otterrò il quarto numero cercato cioè 28 metri di lavoro, che deve essere fatto da 7 operai.
D. Come si opera nel secondo caso?
R. Nel secondo caso conoscendosi un numero determinato di unità ed il valore di una sola di esse unità, si comincierà a cercare il valore di tutte queste unità, moltiplicando tra loro questi due numeri, poscia si dividerà il prodotto pel valore dell’altro numero di unità che si cerca. Il quoziente sarà appunto il numero ricercato.
Così nel proposto esempio conoscendo il numero di più unità, che è 9 metri di panno, ed il valore di una sola che è lire 6, comincierò cercare il valore di tutte, il che ottengo moltiplicando tra loro questi due numeri; 9 metri costeranno 9 volte 6 lire cioè L. 54. Avuto questo prodotto, lo divido per le lire 18 che sono il valore di ciascuna delle nuove unità che cerco, ed {56 [316]} è chiaro che quante volte il 18 è contenuto in 54, altrettanti saranno i metri, che posso comperare. Il quoziente 3 indicherà appunto che con L. 54, potrò avere solo tre metri, se devo pagarli L. 18 ciascuno.
1° Se una pezza dipanno di m. 36 vale 200 lire, quanto varrà un’altra pezza di m. 40?
2° In un giorno 25 muratori fecero 57 m. c. di lavoro; quanto ne faranno operai 15?
3° In 3 giorni 12 operai fecero un lavoro, 36 operai in
quanti giorni lo farebbero?
4° In una fortezza sono 1500 soldati provveduti di viveri
ancora per 6 mesi; quanti soldati si dovranno far uscire per far durare i
viveri due mesi di più?
D. Che cosa s’intende per problema d’interesse?
R. Problemi d’interesse sono quelli, che riguardano il reddito che dà una somma in un determinato tempo, mutuata a un tanto per ogni 100 lire.
Per es. Giovanni imprestò L. 1200 al 5 per 100, cioè col patto che gli vengano pagate L. 5 ogni 100 lire ciascun anno. Si vuol sapere qua! interesse ricaverà annualmente.
D. Quante cose debbonsi considerare nei problemi d’interesse?
R. Sonvi a considerare quattro cose: 1a La somma mutuata, che dicesi capitale; 2a La tassa cioè quel tanto che il debitore deve pagare per ogni 100 lire; 3a Il tempo, cioè il numero di anni, di mesi e di giorni per cui il capitale è mutuato; 4a II frutto che si ricava dal capitale dopo un tempo determinato.
N.B. L’espressione 5 per 100 suolsi scrivere così 5 %, così pure 6 % per esprimere sei per cento.
D. Come si risolvono i problemi d’interesse?
R. Se bene si osserva, si troverà che si riducono {57 [317]} sempre ad uno dei due easi della regola del tre; conosciuto a qoal caso sì riducono, si opera secondo le regole colà date.
Così nel proposto esempio si scorge che si riduce al primo caso della regola del tre, giacchi si conosce il valore ossia l’interesse di un numero determinato di uniti, che cioè 100 lire fruttano L. 5; e si cerca quale sia il valore ossia l’interesse d’un altro determinato numero di unità, cioè di L. 1200. Perciò si cercherà primieramente quanto frutti una lira. Dividendo L. 5 per cento, si troverà che il frutto di una lira è di L. 0,05. Con questo quoziente si moltiplicherà il 1200, così si avrà che l’interesse di L. 1200 al 5 per cento è uguale a lire 60.
Se poi vi fosse da cercare l’interesse di più anni, dopo aver ottenuto l’interesse di un anno, si moltiplicherebbe tale interesse pel dato numero d’anni. Qualora vi fosse da cercare anche l’interesse di mesi o giorni, si può cominciar a cercare l’interesse di un sol mese o di un sol giorno, il quoziente, cioè tale interesse, si moltiplicherà pel numero dei mesi o giorni di cui si cerca l’interesse.
D. Quali sono i problemi di società semplici?
R. Sono quelli che riguardano il modo di far la divisione fra più persone di una somma guadagnata o perduta in società.
D. Che cosa si ha da considerare nei problemi di società semplice?
R. Si devono pure considerare quattro cose: 1a La posta di ciascun socio, cioè quanto ciascun socio ha messo in società; 2a Il capitale sociale, che risulta dalla somma delle poste; 3a La somma perduta o guadagnata, cioè la perdita od il guadagno totale; 4a Quanto tocca a ciascun socio della perdita o del guadagno.
Per es. due mercanti fecero società; uno pose L. 3000, l’altro ne pose 5000. Il guadagno fu di L. 320. Quanto toccherà a ciascuno di questo guadagno? {58 [318]}
D. Come si risolvono questi problemi?
R. Questi problemi si riducono ad altrettanti problemi di regola del tre del primo caso, quanti sono i socii; e però si opera secondo le regole date.
Cosi nel proposto esempio si ha L. 320 frutto di un determinato numero di unità cioè della somma delle due poste, perciò fatta l’addizione delle poste, si comincia a cercare quanto abbia fruttato ciascuna lira messa in società; il che si trova dividendo il frutto per la somma delle poste. Si troverà L. 320 : 800 = 0,04 che è il frutto dato da ciascuna lira. Con questo numero 0,04 si moltiplicherà poi separatamente ciascuna delle poste e così si troverà per la prima posta L. 3000 × 0,04 = L. 120 per frutto; per la 2a posta 5000 × 0,04 = 200 per frutto.
ESERCIZI.
1° Quale interesse darà il capitale di lire 5280 prestato a 6 °/o per 15 anni?
2° Si cerchi l’interesse di 10 mila lire al 5 % per 5 anni e 6 mesi.
3° Quali saranno gli interessi di L. 6000 al 5 % in capo a 25 anni?
4o Un viaggiatore ha speso 3 lire in commestibili e va ad un’ombra per pranzare: soppraggiunge uu suo amico che ne aveva per 5 lire e gli propone di mettere tutto in comune. L’altro accetta; mentre stanno per cominciare il pranzo arriva un terzo che, accettato, pranza con essi. Partendo quest’ultimo lascia loro 8 lire pel cibo e per la cortese accoglienza, affinchè se le dividano i due primi. Quanto tocca a ciascuno?
5° Cinque persone promettono di aiutarsi a vicenda in caso di qualche infortunio, mettendo ciascuno in proporzione delle rispettive entrate. Il primo ha un’entrata annua di L. 1000; il secondo di L. 1200; il terzo di L. 1350; il quarto di L. 1552; il quinto di L. 2000. Un incendio reca al primo un danno di L. 13540. Quanto devono mettere gli altri quattro, supponendo che essi vogliano riparare interamente a questo danno? - Quanto dovrebbero mettere ciascuno degli altri 4, supponendo che l’incendio abbia recato lo stesso danno di L. 13640 al secondo, al terzo, al quarto al quinto? - Quanto dovrebbero mettere in ciascuno di questi casi riparando soltanto la parte convenuta? {59 [319]}
D. Che cosa vuol dire geometria?
R. Geometria è una parola composta di due voci greche (geo- metria) che vuol dire misura della terra; ed ha per oggetto le proprietà e le misure dell’estensione.
D. Quante dimensioni distinguonsi nella estensione finita?
R. Tre: lunghezza, larghezza, profondità o altezza, le quali dimensioni sono attributi essenziali dei corpi.
D. Che cosa è il punto?
R È il limite di una linea privo di ogni dimensione.
D. Che cosa è una linea?
R. E una lunghezza, senza larghezza e profondità.
D. Come si divide la linea?
R. In retta, curva e spezzata.
D. Qual è la linea retta?
R. E il più corto cammino fra due punti.
La linea retta si chiama orizzontale se segue la direzione di un piano d’acqua stagnante. Si chiama verticale se segna la direzione del filo a piombo. Si chiama inclinata se segue altre direzioni.
Due linee si dicono convergenti se tendono ad incontrarsi

Linea retta oriz.
 - linea inclinata
- linea inclinata

 - linee divergenti
- linee divergenti
 - linea verticale
- linea verticale
Queste
medesime linee convergenti da una parte, sono divergenti dall’altra. {60 [320]}
D. Qual’è la linea curva?
R. Qualunque linea non retta, nè composta di linee rette si dice curva.
fig 1.

D. Qual’è la linea spezzata?
R. E quella che è composta di linee rette.
D. Che cosa è la superficie?
R. È un’estensione in lunghezza e larghezza senza profondità.
D. Qual è la più semplice di tutte le superficie?
R. E la piana.
D. Che cosa è il piano?
R. È quella superficie in cui si può adattare in tutti i versi una linea retta.
D. Qual’è la superficie curva?
R. Quella che non è piana ne' composta di superficie piane.
D. Che cosa è il solido o corpo geometrico?
R. E tutto ciò che ha le tre dimensioni di lunghezza, larghezza e profondità.
D. Che cosa è l’angolo.
R. E la vicendevole inclinazióne di due linee rette che s’incontrano in un punto.
fig. 2.
 vertice, angolo, late, late
vertice, angolo, late, late
D. Come si chiama il punto dove le due rette s’incontrano?
R Il vertice o cima dell’angolo. {61 [321]}
D. Come si chiamano le due rette?
R. I due lati.
D. Che cosa è la perpendicolare?
R. È quella retta che incontra un’altra retta in modo che gli angoli contigui od adiacenti siano eguali fra di loro. Questi angoli diconsi retti.
fig. 3.
perpendicolare

D. Qual’è la linea obliqua?
R. E quella retta che cadendo sopra un’altra fa con questa due angoli adiacenti disuguali fra di loro.
fig. 4.
 obligua, ottusang.
adiac, angolo acuto
obligua, ottusang.
adiac, angolo acuto
D. Quali nomi prendono gli angoli adiacenti alla linea obliqua?
R. Quello che è maggiore dell’angolo retto, dicesi ottuso; quello che è minore dicesi acuto.
D. Quand’è che due rette si chiamano parallele?
R. Quando poste in un medesimo piano e prolungate indefinitivamente da ambe le parti non possono incontrarsi.
fig. 5.
 - Linee parallele
- Linee parallele
{62 [322]}
D. Che cosa e una figura piana?
R. È un piano chioso tutto all’intorno da una o più linee.
fig. 6.
 - Figura piana
- Figura piana
D. Che cos’è il perimetro od il contorno della figura?
R. È la somma di tutte le linee che racchiudono la figura.
D. Come si divide la figura?
R. In rettilinea, curvilinea e mistilinea, secondochè le linee, che la comprendono, sono tutte rette o tutte curve o parte rette e parte curve.
figura, curvilinea
D. Come si chiamano comunemente le figure rettilinee ?
R. Poligoni.
D. Come si chiamano le rette del perimetro?
R. Lati. {63 [323]}
D. Qual’è il più semplice di tutti i poligoni?
R. Il triangolo.
D. Come si diridono inoltre i poligoni?
R. In quadrilateri ossia di quattro lati, pentagoni di cinque, esagoni di sei, ettagoni di sette, ottagoni di otto, ennagoni di nove, decagoni di dieci, dodecagoni di dodici, pentedeeagoni di quindici.
D. Come si distinguono i triangoli?
R. Riguardo ai lati e riguardo agli angoli.
D. Quanti sono riguardo ai lati?
R. Sono tre equilatero che ha tutti e tre i lati eguali, isoscele che ne ha due, scaleno che li ha tutti e tre disuguali.
D. Quanti sono riguardo agli angoli?
R. Sono tre: triangolo rettangolo, che ne ha uno
retto: ottusangolo, che ne ha uno ottuso: acutangolo che li ha
tutti e tre acuti.
 - fig.9
- fig.9
 - fig.10.
- fig.10.
triangolo equilatero triangolo
isoscele
 - fig. 11.
- fig. 11.
 - fig. 12.
- fig. 12.
triangolo scaleno triangolo
ottusangolo rettangolo
{64 [324]}
D. Che cosa s’intende per quadrilatero?
R. Una figura piana compresa da quattro linee rette.
D. Come si distinguono i quadrilateri?
R. In quadrati, rettangoli, rombi, romboidi e trapezi.
D. Che cosa è il quadrato?
R. È un quadrilatero che ha tutti i lati eguali e tutti gli angoli retti.
 - fig. 13.
- fig. 13.
quadrato
D. Che cosa è il rettangolo?
R. È un quadrilatero che ha tutti gli angoli retti senza avere tutti i lati eguali.
 - fig. 14.
- fig. 14.
rettangolo.
D. Che cosa è il rombo?
R. È un quadrilatero che ha tutti i lati uguali senza avere tutti gli angoli retti.
 - fig. 15. - rombo
- fig. 15. - rombo
{65 [325]}
D. Che cosa è il romboide?
R. È un quadrilatero che ha solamente i lati opposti ugnali senza essere rettangolo.
 - fig. 16. Romboide
- fig. 16. Romboide
D. Come
si chiamano questi quattro quadrilateri?
R. Parallelogrammi, perchè hanno i lati opposti paralleli fra di loro.
D. Che cosa è il trapezio?
R. È un quadrilatero qualunque non parallelogramma.
 - fig. 17 - Trapezio
- fig. 17 - Trapezio
D. Comunemente quale suolsi chiamare trapezio?
R. Quel quadrilatero che ha solo due lati paralleli, (fig. 17). I trapezi diversi da questi diconsi trapezaidi (fig. 18).
 - fig. 18. - trapezoide
- fig. 18. - trapezoide
{66 [326]}
D. Che cosa è la diagonale?
R. È una retta tirata dentro di un poligono tra i vertici di due angoli non adiacenti ad uno stesso lato.
 - fig. 19. - diagonale
- fig. 19. - diagonale
D. Che cosa è il circolo?
R. È una figura piana terminata da una linea curva che chiamasi periferia o circonferenza, la quale ha tutti i suoi punti egualmente distanti da un punto interno che dicesi centro.
 - fig. 20.
- fig. 20.
D. Che cosa è il raggio del circolo?
R. E qualunque retta tirata dal centro alla periferia.
D. Che cosa è il diametro di un circolo?
R. È qualunque retta che passa pel centro, ed è terminata da ambe le parti alla circonferenza. {67 [327]}
D. Che cosa è un arco?
R. Una parte qualunque della circonferenza.
D. Che cosa è la corda f
R. È la retta che unisce le due estremità dell’arco.
D. Che cosa è il segmento P
R. La parte del circolo compresa tra l’arco e la corda
 - fig 21. - arco.
- fig 21. - arco.
Segmente
maggiore
D. Che cosa è la saetta?
R. E la retta che divide l’arco e la corda in due parti eguali.
D. Che cosa è il quadrante?
R. E un arco eguale al quarto della circonferenza. {68 [328]}
D. Che cosa è corpo geometrico o solido?
R. Corpo geometrico o solido è l’estensione considerata sotto tre dimensioni, lunghezza, larghezza, altezza.
D. Che cosa è il volume di un corpo?
R. Volume di un corpo è il corpo stesso, o anche lo spazio, che esso occupa o si suppone occupare.
D. Quante sorta di solidi vi sono?
R. Due sorta, solidi poliedri, e solidi rotondi,
D. Quali solidi si dicono poliedri e quali rotondi?
R. Si dicono solidi poliedri quelli le cui superficie sono tutte piane, rotondi quelli che hanno una superficie curva.
D. Quali sono i principali solidi poliedri?
R. Sono il cubo il prisma e la piramide.
D. Quali sono i principali solidi rotondi?
R. Sono il cilindro, il cono e la sfera.
D. Che cosa è il cubo?
R. II cubo è un corpo terminato da sei superficie uguali e quadrate.
 - fig. 22.
- fig. 22.
Cubo
{69 [329]}
D. Che cosa è il prisma?
R. Il prisma è un còrpo terminato all’estremità da due poligoni opposti eguali e paralleli che si chiamano ‘basi, e lateralmente da tanti parallelogrammi quanti sono i lati di ciascuna base.
 - fig. 23.
- fig. 23.
D. Che
cosa è la piramide?
R. La piramide è un solido terminato da un poligono qualunque, che gli serre di base, lateralmente da tanti triangoli, che concorrono in un punto detto vertice, quanti sono i lati della base.
 - fig. 24. - Piramide.
- fig. 24. - Piramide.
{70 [330]}
D. Che cosa è il cilindro?
R. Il cilindro è un solido che ha per basi due circoli eguali e paralleli ed è lateralmente terminato da una superficie curva, che può svolgersi in piana.
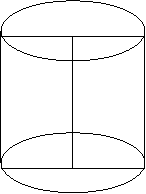 - fig 25.
- fig 25.
D. Che cosa à il cono?
R. Il cono è un solido terminato alla base da un circolo e lateralmente da una superficie curva, che finisce in un punto detto vertice del cono.
 - fig.
26. - Cono
- fig.
26. - Cono
{71 [331]}
D. Che cosa è la sfera?
R. La sfera è un solido terminato da una sola superfìcie curva, i coi ponti sono egualmente distanti da un punto interno detto centro.
 - fig.
27. - Sfera.
- fig.
27. - Sfera.
D. Qual è il modo più facile per farci un’idea chiara del nuovo sistema metrico decimale?
R. Per farci un’idea chiara dei nuovi pesi e delle nuove misure bisogna osservare quali pesi e quali misure vengano sostituiti agli antichi, e quale ne sia il vicendevole loro rapporto, perciò sarà di massima utilità il leggere le seguenti tavole, delle quali si potrà tener sott’occhio quella che riguarda la propria provincia. {72 [332]}
Tavole
dei numeri fissi per convertire le misure antiche in misure nuove e
reciprocamente colla semplice moltiplicazione.
|
DISTINZIONE DELLE MISURE
|
FATTORI o numeri fissi per
|
RIDURRE
LE MISURE ANTICHE
in
nuove cioè
|
NUMERO DI CIFRE da separare NEL PRODOTTO
|
FATTORI o NUMERI FISSI per
|
RIDURRE
LE MISURE NUOVE IN ANTICHE cioè
|
NUMERO DI CIFRE da separare NEL PRODOTTO
|
|
LINEARI
|
2·5
3·09
·514
1·715
·6
|
Le miglia in
chilometri...
trab. in metri.
I piedi in metri.
Le teste in
metri.
I rasi in metri
|
una
due
tre
tre
una
|
·4
·324
1·944
·583
1·57
|
I chilometri in
miglia...
I metri in trab
I metri in piedi.
I metri in tese
I metri in rasi
|
una
tre
re
tre
due
|
|
DI SUPERF.
|
9·526
·265
·38
·381
|
I trab quadr. in
metri quad.
I piedi quadr. in
metri quadr.
Le gior. in ett.
Tavole in are.
|
tre
tre
due
tre
|
·105
3·779
2·625
2·62
|
I metri quadr. in
trab. quadr.
I piedi quadr in
metri quad
Le ettare in
gior.
Are in tavole
|
tre
tre
tre
due
|
|
DI SOLIDITÀ
|
29·401
·136
5·041
4·033
4·08
|
I trab. cubi in
metri cubi...
I piedi cubi in
metri cubi...
Le teste pel
fieno in steri...
Le tese per legna
in steri..
Trab. camerale in
metri cubi...
|
tre
tre
tre
tre
tre
|
034
7·35
1·198
·248
0·245
|
I metri cubi in
trab. cubi...
I metri cubi in
piedi cubi..
Gli steri pel
fieno in tese..
Gli steri per
legna in steri
I metri cubi in
trab. camerali...
|
tre
due
tre
tre
tre
|
|
DI CAPAC.
|
·23
·5
2·3
|
Le emine in
ettolitri...
Le brente in
ettolitri...
Emina in decal.
|
due
una
una
|
4·34
2·
·435
|
Gli ettolitri in
emine...
Gli ettolitri in
brente...
Decalitri in em.
|
due
due
tre
|
|
PESI
|
·9222
9·223
·369
·306
|
I rubbi in
miriagrammi..
Rubbi in kilog.
Le libre in
kilogrammi...
Le oncie in
ettogrammi...
|
quattro
tre
tre
tre
|
1·0853
·1085
2·711
3·253
|
I miriagr. in
rubbi...
Kilogr. in
rubbi...
I kilogr. in
libre
Gli ettogr. in
oncie...
|
quattro
quatt.
tre
tre
|
{73 [333]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
di METRICHE
NUMERI
FISSI
|
METRICHE
IN
ANTICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lung.
di sup.
di cap.
Pesi
Monete
|
Bracc.
Piede
Pert. q.
Mogg.
Soma
Brenta
Libbra grossa
Lib. pic.
Marco
L. Austrica
Fior.
|
0,594936 m.
0,435185 m.
6,545179 Are.
1,465136 El.
1,645136 El.
0,755544 El.
0,762517 Cg
0,326793 Cg.
0,234997 Cg.
0,866 Cg.
|
1,680852 M.
2,297873 M.
0,152784 Ara.
0,683834 El.
0,607792 El.
1,323550 El.
1,311446 Cg.
3,060040 Cg.
4,255370 Cg.
|
di 12 once,
l’oncia di 12 punti
6 piedi fanno un
trabucco.
di 24 tav. che
fan 3456 piedi q.
di 8 staia, lo
staio di 4 quartari.
di 9 staia, lo
staio di 4 quartari.
= 48 pinte= 96
boc. = 3 staia, lo staio di 2 cm. l’emina di 2 q.
di 28 once.
di 12 once.
di 8 once.
di 100 centesimi
di 2 metà, la metà di 2 quarti
|
{74 [334]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
IN
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup
di cap.
di peso
Monete
|
Braccio
Piede
Passo q.
Campo
Moggio
Secchio
Libbra gr.
Libbra sott
le
stese della
|
0,6851
0,6384 m
0,347398 m
0,030171 Are
36,5661 Are
0,800 El.
0,1080 El.
0,476998 Cg.
0,302025 Cg.
Lombardia
|
di 12 once,
l’oncia di 12 punti, il punto di 12 atomi; 5 piedi fanno il passo.
di 25 piedi q.
di 4 staia, lo
staio di 4 quarti, il quarto di 4 quartaroli.
di 4 bozze, la
bozza di 4 quartuzzi; 48 secchi fanno l’anfora.
di 12 once,
l’oncia di 8 dramme.
di 12 once,
l’oncia di 144 carati.
|
{75 [335]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
IN
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup.
di cap.
di peso.
Monete
|
Piede
Braccio
Tornatura
Corba(G.)
Corba
Libbra
Scudo
|
0,380098 m.
0,040039 m.
20,804358 Are.
0,7864 El.
0,7859 El.
0,361850 Cg.
5,30 L.
|
di 12 once,
l’oncia di 12 punti.
La pertica era di
12 piedi.
di 20 once.
di 144 pertiche
q. o tavole, la tavola di 100 piedi q.
= 2 staia =
8quartiroli - 32 quarticini.
di 4 quartarole,
la quartarola di 15 boccali, il boccale di 4 fogliette.
di 12 once,
l’oncia di 8 ottavi l’ottavo di 20 carati, il carato di 4 grani.
di 10 paoli, il
paolo di 10 baiocchi, il baiocco di 5 quattrini.
|
|
MISURE
|
UNITÀ
principali
|
ANTICHE
IN
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup.
di cap.
di peso
Monete
|
Palmo
Cannella
Emina (G).
Barile da vino
Barile da olio
Libbra gr.
Libbra sott.
Lira antica
|
0,24803 m.
0,088625 Are.
1,2072 El.
0,7423 El.
0,6548 El.
0,348456 Cg.
0,316678 Cg.
0,84 L.
|
di 12 once,
l’oncia di 12 punti,
il punto di 12
atomi.
di 12 palmi
superficiali, il palmo di 12 once superficiali
di 4 staia, lo
staio di 8 ottavi
di 90 amole; 2
barili fanno la
mezzarola.
di 4 quarti.
di 12 once; 25
libbre fanno il Rubbo, 6 rubbi il Cantaro
|
Nota. Ad alcune misure di capacità si unisce un (G) per indicare che servono solo per le granaglie e non pei liquidi. {76 [336]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
in
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup.
di cap.
di peso.
Monete
|
Trabucco
Raso
Starello
Starello (G)
Pinta
Libbra
Lira antica
|
3,14820 m.
0,5993 m.
39,867 Are.
0,48961 El.
0,8968 El.
0,398985 Cg.
1,88 L.
|
di 12 palmi, il
palmo di 4 quarti
di 19 imbuti.
di 12 oncie.
|
|
MISURE
|
UNITÀ
principali
|
ANTICHE
IN
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup.
di cap.
di peso
Monete
|
Pertica
Braccio da seta
Braccio da tela
Biolca
Staio (G).
Crenta
Rubbo
Lira vecch
|
3,27100 m.
0,58775 m.
0,6395 m.
30,814390 Are.
0,4704 El.
0,71672 El.
8,2000 Cg.
0,20 L.
|
di sei braccia da
muro, il braccio di 12 oncie,di l’oncia di 12 punti.
6 staia, lo staio
dividesi In tav., piedi e oncie sempre di 12 In 12 (la tavola è di 4 pertiche q.).
di due mine, la
mina di 8 quartarole
di 36 pinte, la
pinta di due boccali.
di 25 libbre, la
libbra di 12 oncie, l’oncia di 24 danari, il danaro di 24 grani.
di 20 soldi.
|
{77 [337]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
in
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh
di sup.
di cap.
di peso
Monete
|
Piede
Braccio
Biolca
Staio (G.)
Quartaro
Peso
Lira vecch.
|
0,523048 m.
0,633150 m.
28,364724 Are.
0,6325 El.
1,01812 Are.
8,511125 Cg.
0,305 L.
|
di 12 once; 6
piedi fanno il carezzo o pertica.
di 12 once.
di 72 tavole, la
tav. di 4 cavezzi q.
di due mine, la
mina di 4 quarti.
di 90 boccali.
di 25 libbre, la
lib. di 12 once, l’oncia di 12 ferlini.
di 20 soldi, il
soldo di 12 danari.
|
{78 [338]}
|
MISURE
|
UNITÀ
principale
|
ANTICHE
in
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup.
di solid.
di cap.
di peso
Monete
|
Braccio
Quadrato
Stioro
Brac. cubo
Moggio (G)
Barile da vino
Barile da olio
Libbra
Lira vecch
Scudo
Fiorino
|
0,583660 m.
34,061912 Are.
6,2341 Are.
0,19882 mc.
5,847087 El.
0,455840 El.
0,334289 El.
0,339542 Cg.
0,840 L.
5,88 L.
1,400 L.
|
di 12soIdi, il
soldo di 12 danari; 5 braccia fanno la canna agrimensoria
si suddivide in
tavole, pertiche, deche di 10 in 10; la deca vale 10 braccia q.
di 12 panore, il
pan. di 12 pugnora: il puguoro vale braccia 987.
di 6 bracciuole,
la brace, di 12 once: 12 bracciole fanno il traino misura pèl legname da
costruzione, e 12 braccia cube fanno la catasta misura pel legname da ardere.
di 8 sacca, il
sacco di 3 staia, lo staio di 4 quarti, il quarto di 8 mezzette, la mezz. di
2 quartucci.
di 20 fiaschi, il
fiasco di 4 mezzette, la mezzetta di 2 quartucci.
di 16 fiaschi, il
fiasco di 4 mezzette, la mezzetta di 2 quartucci.
di 12 once,
l’oncia di 24 denari, il denaro di 24 grani.
di 20 soldi, il
soldo di 12 danari.
di 100 quattrini,
il quattrino di 4 denari.
|
{79 [339]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
in
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup
di cap.
di peso
Monete
|
Palmo
d’architetto
Palmo mercantile
Piede
Pezza
Rubbio(G.)
Barile da vino
Barile da olio
Libbra
Scudo
|
0,223422 m.
0,249 m.
0,297896 m.
26,4063 Are.
2,944651 El.
0,5834159 El
0,5748059 El
0,339072 Cg.
5,36 L.
|
di 12 onde
l’oncia di 5 minuti, 10 palmi fanno la canna, lo staiuolo vale palmi 5,75, la
catena 57,50
 4 del palmo d’archit.: 5 piedi fanno il 3 passo e 1000
passi il miglio 4 del palmo d’archit.: 5 piedi fanno il 3 passo e 1000
passi il miglio
= 6 catene q. = 4
quarte, la quarta è di 40 ordini, l’ordine di 10 staiuoli.
= 4 quarti, il
quarto di 4 scorzi, lo scorzo di 2 quartucci.
di 28 boccali, il
boccale di 24 fogliette; la botte è di 16 barili.
di 12 once,
l’oncia di 8 ottavi, l’ott. di tre denari, il denaro di 24 grani; 100 libbre
fanno il quintale, 10 quintali il migliaio
di 10 paoli, il
paolo di 10 baiocchi, il baiocco di 5 quattrini.
|
{80 [340]}
|
MISURE
|
UNITA
principali
|
ANTICHE
in
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
Linear.
|
Pes
|
0,296310 m.
|
palmi minoro =
1,333.... del palmus maior = 12 unciae - 0,2 del postili maior =. 0,4 del
gressus = 0,666... del cubitus. Lo stadium è di 625 piedi, l’aetus di 120 e
il milliarum di 5000.
|
|
di sup.
|
Iogerum
|
25,2839 Are.
|
= 2 aetus = 1/2
dell’heredium = 800 = 1/2 della centuria = 1/800 del
saltus. Il iugero ha l’area di 28,80 piedi q.
|
|
di cap
|
Congius (G.)
|
0,3240 El.
|
= 6 sextarii = 12
heminae = 1/8 = dell’amphora.
|
|
|
Amphora
|
0,25920 El.
|
= 2 urniae
= 3 modii = 6 semodii = 1/20 del culeus.
|
|
di peso
|
Libra o as o
pondo.
|
0,327182 Cg.
|
di 12 unciae; il
talentum è di 80 libbre. Le altre misure di peso sono di 2, 3, 4, 5, 6, 7, 8,
9, 10, 11 once, e di 3, 4, 5, 10, 100 assi; come indicano chiaramente i loro
nomi stessi.
|
|
Monete
|
Asse librale
|
0,05 L.
|
= 2 semisses
= 3 trientes = 4 guadrantes = 1/10 del
denarius = 1/5 del quinarius = 0,4 del semistertius. Le
ultime tre monete erano di argento e cominciarono a coniarsi nel 485 di Roma;
l’asse invece e le sue suddivisioni erano di rame, e sono le monete più
antiche dei Romani.
|
|
|
Sesterzio
|
0,20 L.
|
Unità d’uso dopo
l’anno 563. Il seslertiutnorum, cioè sesstertiorum millia,
valeva 1000 sesterzii, che fanno 200 lire italiane.
|
{81 [341]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
IN
METRICHE
NUMERI FISSI
|
SUDDIVISIONI
|
|
di lung.
di sup.
di cap.
di peso
Monete.
|
Palmo
Moggio
Tomolo (G).
Barile
Rotolo
Libbra
Ducato
|
0,2651503 m.
0,998684 Are
0,5554511 El.
0,4362503 El.
0,890997 Cg
0,3207589 Cg
4,25 L
|
1
= - di un minuto
primo del grado medio
700
del merid.
terrestre, si divide in dec. cent.; 10 palmi fanno una canna.
= 100 canne q.,
si divide in parti decimali.
= 3 palmi cubi.,
si divide in 2 mezzette, la mezzetta in 2 quarti, il quarto in 6 misure
di 60 caraffe,
equivale a tre palmi cilindrici cioè ad un cilindro retto, largo un palmo e
alto tre ( 16 barili fanno la botte).
si divide in
parti dee. I millesimi si chiamano trapesi (100 rotoli fanno un cantaio)
di 12 once.
di 10 carlini, il
carlino di 10 grana, i 1 gr. di 12 cavalli.
|
{82 [342]}
|
MISURE
|
UNITÀ
principali
|
ANTICHE
in
METRICHE
NUMERI
FISSI
|
SUDDIVISIONI
|
|
di lungh.
di sup
di cap.
di peso
Monete
|
Palmo
Salma
Tomolo(G.)
Quartaro
Rotolo
Oncia
|
0,258098 m.
174,625873 Are.
0,1719305 El.
0,1719305 El.
0,79342Cg.
12,75 L.
|
di 12 once,
l’oncia di 12 linee, la linea di 12 punti.La canna è di 8 palmi.
si divide in
bisaccie, tomoli, mondelli, carozzi e quarti, sempre di 4 in 4; il quarto è di 4 canne q.
= 1 palmo cubo;
si divide in mondelli, carozzi, quarti e quartigli di 4 in 4; (16 tomoli fanno la salma).
= 1 palmo cubo;
si divide in 20 quartucci, il quarluccio in 2 caraffe, la caraffa in due
bicchieri, un barile vale 2 quartari, la botte 32.
di 30 once,
l’oncia di 8 dramme, la dramma di 3 scrupoli, lo scrup, di 20 grani, il grano
di 8 ottavi; ( 12 once fanno la libbra, 100 rotoli il cantaio)
di 30 tari, il
tari di 20 grani, il grano di 6 piccoli. Un tari siciliano vale un carlino di
Napoli.
|
{83 [343]}
Maniera
di ridurre le Misure Antiche in Misure Metrico-dceimali e reciprocamente,
secondo il modello esposto nelle precedenti tavole.
D. In che maniera le misure del sistema antico si possono ridurre in misure nuove e reciprocamente?
R. Cercato il numero fisso, questa riduzione si fa per mezzo della moltiplicazione,
D. Che cosa s’intende per numero fisso?
R. Per numero fisso s’intende il rapporto che passa tra il peso o la misura di un sistema coll’altro. Per esempio se io voglio cercare il numero fisso, ovvero il rapporto del piede col metro, dirò: il piede eguaglia metri 0,514. Questo 514 (che sono millimetri) è numero fisso, ovvero è quella parte del metro che corrisponde alla lunghezza del piede. Volendo cercare il rapporto del metro col piede, dirò: il metro eguaglia piedi 1,944, vale a dire il metro vale un piede, più novecento quarantaquattro millesime parti del piede. Il numero 1,944 è numero fisso.
D. Quale altra cosa si deve osservare pei numeri fissi?
R. Conviene ancora notare che avendo da ridurre intieri e frazioni del sistema antico, per abbreviare si riducono gli interi maggiori in minori: per esempio occorrendo rubbi, libbre e oncie, si ridurranno i rubbi in libbre; poscia tutte le libbre, in oncie; indi se ne farà la debita riduzione coi pesi del nuovo sistema.
D. Dato il numero fisso, come si possono ridurre le misure di un sistema colle misure dell’altro?
R. Dato il numero fisso, si riducono le misure di un sistema nell’altro colla moltiplicazione, moltiplicando {84 [344]} cioè il numero fisso pel numero della merce, che si vuol ridurre, seguendo in ogni cosa le regole di moltiplica decimale.
ESEMPIO: Quanti metri fanno piedi 45?
Operazione.
|
Numero fisso o
moltiplicando
|
0,514
|
|
Numero da ridursi
o moltiplicatore
|
45
|
|
|
2570
|
|
|
2056
|
|
|
23,130
|
Spiegazione. Il numero 514 sono millimetri che formano la lunghezza del piede relativamente al metro, 45 sono piedi da moltiplicarsi pel suo rispettivo numero 514. Nel prodotto si separeranno tre cifre di frazioni; onde si dirà: 45 piedi fanno 23 metri, più 130 millimetri, ovvero 13 centimetri.
D. Come si fa la prova di queste operazioni?
R. La prova di queste operazioni si eseguisce perfettamente colla regola di mettere un fattore al posto dell’altro e ripetere la moltiplicazione
Esercizi
sulle Tavole per la conversione delle Misure.
1. Quanti
metri fanno 27 trabucchi?
Quanti trabucchi, piedi ed oncie fanno 50 metri?
A quante ore equivalgono 7 giornate?
2. Quanti
metri fanno 5 braccia milanesi?
Quante some fanno 7 ettolitri?
Quante lire valgono 13 fiorini?
3. Quanti
piedi fanno 27 metri? Quante are fanno 3 campi?
4. Quante
emine fanno 27 ettolitri?
Quanti ettogrammi fanno due libbre grosse? {85 [345]}
5. Quanti
metri fanno 27 rasi?
Quante pinte fanno 5 ettolitri?
6. Quante
are fanno 32 biolche?
A quanti rabbi equivalgono 2 chilogrammi?
7. Quante
lire fanno 5 lire vecchie?
Quanti soldi fanno 27 lire?
8. Quanti
chilogrammi fanno 5 libbre?
Quante libbre fanno 2 chilogrammi?
9. Quante
are fanno 123 tornature?
Quante oncie fanno 3 chilogrammi?
Quanti scudi fanno 27 lire?
10. Quante
are fanno 5 catene q.?
A quante libbre equivalgono 7 ettogrammi?
11. Quanti
congi erano necessari per fare 5 ettol.?
Quanti sesterzi fanno 20 lire?
12. Quanti
tomoli ci vogliono per 7 ettolitri?
Quanti carlini ci vogliono per fare 1 lira?
13.
Quanti metri fanno 15 palmi?
Quanti tari fanno 83 centesimi? {86 [346]}
ITALIA.
Provincie
Sarde.
|
Quadruplo di
Genova
|
L. 70 00
|
|
Carlino
|
50 00
|
|
Doppia di Savoia
|
28 45
|
|
Doppietta
|
10 00
|
|
Scudo vecchio
|
7 10
|
|
Scudo di Sardegna
|
4 80
|
|
Lira
|
100
|
|
Reale
|
0 48
|
|
Soldo
|
0 05
|
Provincie
di Lombardia.
|
Fiorino Austriaco
|
2 47
|
|
Lira Austriaca o
svanzica nuova
|
0 86
|
|
Svanzica vecchia
|
0 83
|
|
Carantano
|
0 03
|
{87 [347]}
Provincie
di Parma.
|
Doppia
|
21 92
|
|
Ducato
|
5 15
|
|
Lira vecchia
|
020
|
|
Soldo
|
0 01
|
Provincie
di Modena.
|
Scudo d’Ercole
III
|
5 60
|
|
Scudo di
Francesco III
|
5 54
|
|
Ducato
|
2 80
|
|
Scudo dell’Aquila
|
1 42
|
|
Quarantana
|
0 65
|
|
Lira di Modena
|
0 305
|
|
Soldo o bolognino
|
0 015
|
Provincie
di Toscana.
|
Francescone
|
560
|
|
Scudo Fiorentino
|
5 88
|
|
Pezza livornese
|
4 83
|
|
Franceschino
|
2 80
|
|
Fiorino
|
1 40
|
|
Lira vecchia
|
0 84
|
|
Lira lucchese
|
0 75
|
|
Soldo vecchio
|
0 042
|
|
Soldo lucchese
|
0 37
|
Provincie
della Romagna, Umbria e Marche.
|
Doppia
|
17 07
|
|
Scudo
|
5 32
|
|
Testone
|
1 59 {88 [348]}
|
|
Papetto
|
1 06
|
|
Paolo
|
0 532
|
|
Grosso o mezzo
paolo
|
0 266
|
|
Baiocco
|
0 053
|
Provincie
di Sicilia e Napoli.
|
Onza
|
12 75
|
|
Piastra
|
5 10
|
|
Ducato
|
4 25
|
|
Carlino
Napoletano
|
0 425
|
|
Tari siciliano
|
0 425
|
FRANCIA.
|
Scudo
|
5 80
|
|
Luigi
|
3 55
|
|
Lira antica detta
tornese
|
0 99
|
INGHILTERRA.
|
Lira sterlina
|
25 208
|
|
Dollaro
|
5 41
|
|
Scellino
|
1 2604
|
|
Penny (Pence)
|
0 105
|
|
Farthings
|
0 026
|
AUSTRIA.
|
Tallero
|
5 19
|
|
Risdallero
|
496
|
|
Fiorino
|
2 59
|
|
Lira
|
0 867
|
|
Kreutzer
|
0 043 {89 [349]}
|
PRUSSIA.
|
Scodo o
risdallero o tallero
|
3 71
|
|
Silbergroschen
|
1 20
|
RUSSIA.
|
Rublo
|
400
|
|
Solotnik
|
100
|
|
Dolo
|
0 047
|
SPAGNA.
|
Piastra
|
5 43
|
|
Reale di Piata
|
0 54
|
|
Realino
|
0 27
|
PORTOGALLO.
|
Cruzada
|
2 95
|
|
Testone
|
0 61
|
|
Reis
|
0006
|
MONETE
ANTICHE GRECIA.
|
Talento Attico
d’oro
|
55608 98
|
|
Talento d’argento
|
5560 89
|
|
Talento d’Egina o
di Corinto 9268 17 cornine, il 2° secolo avanti C
|
5222 41 {90
[350]}
|
ROMA.
|
Aureus o
solidus
|
20 38
|
|
Denarius
|
0 81
|
|
Quinarius
|
0 40
|
|
Sestertias o
nummus
|
0 20
|
|
Dupondius
|
0 16
|
|
As, libella, o
assi pondius fino al336di R
|
0 08
|
|
As, libella, o
assi pondius fino al 720di R
|
0 05
|
|
Sembella prima
del 536 di Roma.
|
0 04
|
|
Teruncius
|
0 02
|
|
Sembella dopo il
536 di R
|
0 025
|
|
Teruncius
|
0 015
|
|
Denaro sotto
Augusto
|
0 79
|
|
Tiberio e Claudio
|
0 78
|
|
Nerone Galba e
Domiz
|
0 73
|
|
Il Talento di
Babilonia valeva
|
7407 38
|
|
Il Talento di
Mosè
|
6172 {91 [351]}
{92 [352]}
|
|
Al benevolo
lettore
|
pag 3
|
|
I - Nozioni
preliminari e numerazione
|
5
|
|
Esercizi sulla
numerazione
|
10
|
|
II -
Dell’Addizione
|
ivi
|
|
Esercizi
sull’addizione
|
12
|
|
III - Della
Sottrazione
|
13
|
|
Esercizi sopra la
sottrazione
|
15
|
|
IV - Della
Moltiplicazione
|
16
|
|
Esercizi sulla
moltiplicazione
|
20
|
|
V - Della
Divisione
|
ivi
|
|
Esercizi sulla
divisione
|
24
|
|
VI - Dei numeri
decimali
|
25
|
|
Esercizi sulla
numerazione decimale
|
26
|
|
VII -
Dell’Addizione decimale
|
27
|
|
Esercizi
|
ivi
|
|
VIII - Della
Sottrazione decimale
|
28
|
|
Esercizi
|
ivi
|
|
IX - Della
Moltiplicazione dei decimali
|
29
|
|
Esercizi
|
30
|
|
X - Della
Divisione decimale
|
ivi
|
|
Esercizi
|
33 {93 [353]}
|
|
Del sistema
metrico decimale.
|
|
|
XI - Nozione
Generale di questo sistema
|
pag 33
|
|
XII - Uniti
fondamentali
|
34
|
|
XIII - Multipli e
sottomultipli decimali
|
36
|
|
XIV - Lettura e
scrittura dei numeri esprimenti misure metriche decimali
|
38
|
|
XV - Delle frazioni
ordinarie
|
41
|
|
§ 1 Riduzione
delle frazioni ai minimi termini
|
45
|
|
§ 2 Riduzione
delle frazioni allo stesso denominatore
|
46
|
|
§ 3
Dell’Addizione delle frazioni
|
48
|
|
Esercizi
|
ivi
|
|
§ 4 Della
sottrazione delle frazioni
|
49
|
|
Esercizi
|
50
|
|
§ 5 Della Moltiplicazione
delle frazioni
|
ivi
|
|
Esercizi
|
51
|
|
§ 6 Della
Divisione delle frazioni
|
ivi
|
|
Esercizi
|
52
|
|
§ 7 Dei numeri
complessi e riduzione dei medesimi in frazione ordinaria e decimale e
viceversa
|
53
|
|
XVI - Della
regola del tre
|
55
|
|
XVII -
Applicazioni della regola del tre nei problemi d’interesse e di società
semplici
|
57
|
|
Esercizi
|
59
|
|
XVIII -
Definizione delle fig geometriche più importanti
|
60
|
|
XIX - Geometria
solida
|
69
|
Appendice Ia.
|
Tavole dei numeri
fissi e maniera di usarle
|
72
|
|
Tavole dei numeri
fissi per convertire le misure antiche in misure nuove e reciprocamente colla
semplice moltiplicazione
|
73
|
|
Maniera di
ridurre le misure antiche in misure metricodecimali e reciprocamente secondo
il modello esposto nelle precedenti tavole
|
84
|
|
Esercizi sulle
tavole per la conversione delle misure
|
85
|
Appendice IIa.
|
Confronto fra le
monete di varii Stati d’Europa e delle Provincie d’Italia colla lira nuova o
franco
|
87
{94 [354]} {95 [355]} {96 [356]}
|